Roues Incrémentales

[Karoup]

Bonjour à tous,
Je fais face à un problème que je n'arrive pas à résumer à un système d'équations ou à toute autre forme.
Voici le concept :

J'ai trois roues incrémentales A, B et C, chaque roue est numérotée sur son contour de 0 à 9. Comme des roues à code de coffre-fort.

Lorsque qu'on fait pivoter la roue A de un cran, la roue B tourne de X crans.
Lorsque qu'on fait pivoter la roue B de un cran, la roue C tourne de Y crans.
Lorsque qu'on fait pivoter la roue C de un cran, la roue A tourne de Z crans.

Si je dis (par exemple) que initialement toutes les roues sont à 1. A doit être sur le chiffre 3, B sur 1 et C sur 9, Existe t-il un calcul qui permettrait de savoir d'avance qu'en tournant i fois la roue A puis j fois la roue B et enfin k fois la roue C j'arriverai à ce résultat ?

J'espère avoir correctement expliqué le modèle. Je n'arrive pas à le représenté, ça parait pourtant simple en l'écrivant...

Merci pour votre aide et à bientôt

[catamat]

Bonjour
Si j'ai bien compris le truc la roue A partant de 1 et arrivant à 3 a tourné de 2 crans (modulo 10) de même B a tourné de 0 crans et C de 8 crans toujours modulo 10.

Supposons que la roue A soit tournée de a crans, la roue B de b crans et la roue C de c crans.

En fait du fait des interactions

A tourne de a+cZ cran, B de b+aX crans et C de c+bY crans.

Donc
a+cZ=2 (mod 10)
b+aX=0 (mod10)
c+bY=8 (mod10)

si c'est ça, reste à résoudre le système.

[Ben314]

Salut,
A la limite, on peut noter que le système donné par catamat correspond à la matrice dont le déterminant est et, si on veut que le système ait systématiquement une unique solution (quelque soient les valeurs de départ et celles désirées à l'arrivé), il faut et il suffit que ce déterminant soit inversible modulo 10, donc que le produit 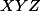soit congru à 0, 2, 6 ou 8 modulo 10.