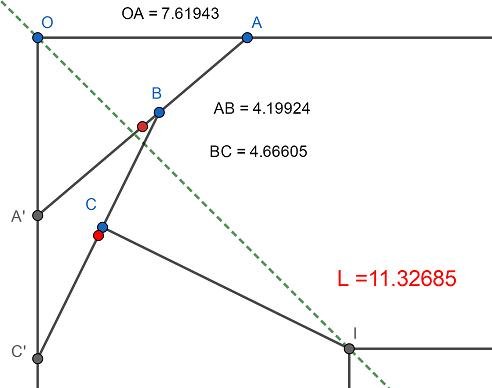
Je veux accéder à l'ilot central en noir qui est un carré de 100m de coté en partant d'un point sur la circonférence de la figure également en noir. Malheureusement, je dois traverser un fossé de largeur L avec de l'eau infesté de piranhas donc je ne peux y aller à la nage (je me retrouve toujours dans des situations impossibles
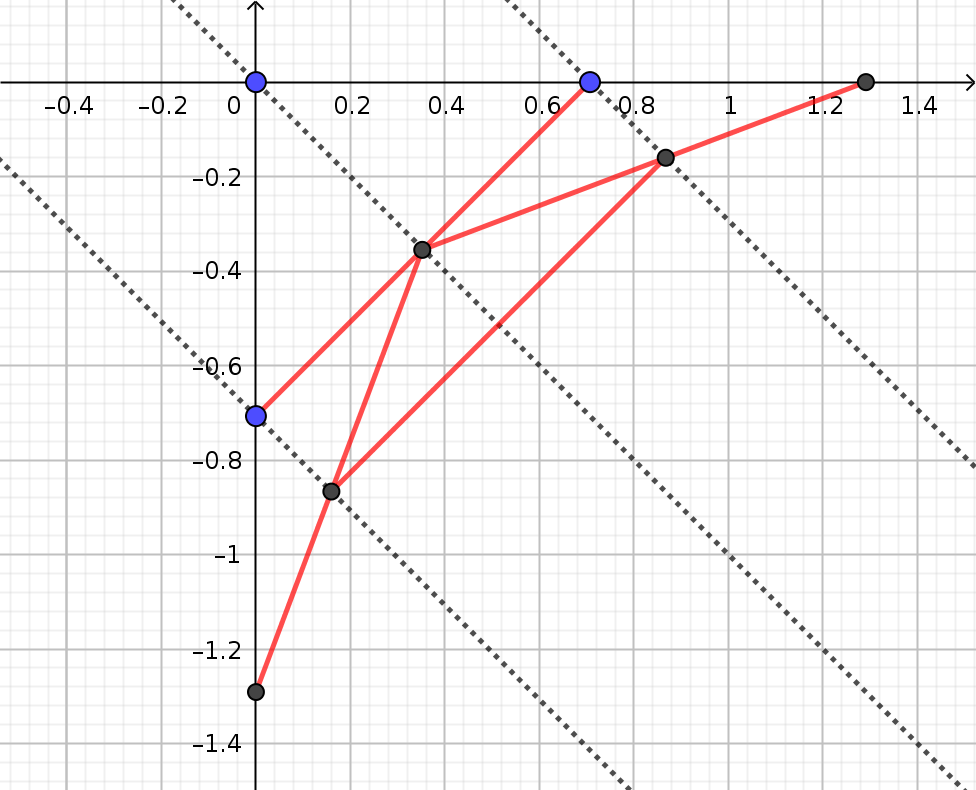
J'ai n planches de longueur 10m assimilées à des segments que je vais utiliser pour construire un pont.
Quelle est la distance L maximale que je peux franchir ? On peut considérer que le recouvrement nécessaire à chaque extrémité des planches pour la solidité du pont est assimilé à un point.
On cherchera d'abord pour n allant de 1 à 5 puis, si le cœur vous en dit, on pourra tenter une limite.
Bon courage et bon amusement j'espère