Peindre au cache !

[Imod]

Bonjour every body

J'ai proposé il y a quelque temps un sujet de peinture à la souris ( toujours sans réponse :--: ), en voici un autre avec peinture au cache :id:

On dispose d'un échiquier usuel colorié en noir et blanc n'importe comment et de deux caches carrés de tailles 3X3 et 4X4 . On peut poser les caches sur les cases de l'échiquier ( proprement ) , ce qui a pour effet d'inverser la couleur de chaque case recouverte , et ceci autant de fois que l'on veut . Peut-on de cette façon obtenir un échiquier tout noir ?

Pour les plus courageux : et si on change la taille de l'échiquier , celle des caches , le nombre de caches :doh:

Imod

[Doraki]

Il y a 5*5 manières de placer un cache de taille 4*4 et 6*6 manières de placer un cache de taille 3*3.
Comme utiliser 2 fois un même cache au même endroit revient à ne rien faire,
il y a donc au plus 2^(25+36) = 2^61 coloriages possibles avec les caches.

Or, il y a 2^64 coloriages possibles de l'échiquier, donc on ne peut pas toujours inverser le coloriage et obtenir un coloriage tout noir.

Sur un échiquier plus grand, avec des caches plus petits, ou avec plus de caches, cet argument ne permet plus de voir que c'est impossible, donc ptetre que c'est possible (mais ça doit demander de gros calculs)

[Imod]

Oui Doraki , c'est la bonne argumentation :++:

Imod

[Doraki]

Est-ce que pour un échiquier assez grand, on peut obtenir tous les coloriages avec des caches 3*3 et 4*4 ? J'en doute..

J'ai essayé d'obtenir une case noire seule dans le coin d'une grille de taille 9*9 mais c'est impossible. Et pour 10*10.. bah le calcul est très long, et au delà je dois changer d'algo (O(2^(n²)) c'est pas super).

[Doraki]

Si on pave la grille en répétant ce motif :

Code: Tout sélectionner

........
**..**..
**..**..
........
**..**..
**..**..

Alors on voit que chaque cache 3*3 et chaque cache 4*4 contient un nombre pair de cases étoilées. Et donc un coloriage colorie toujours un nombre pair de cases étoilées.

Donc on ne peut pas obtenir un coloriage qui colorie seulement une case, donc a fortiori on ne peut pas obtenir tous les coloriages quelle que soit la grille.

Ca marche avec n'importe quelle taille de grille et n'importe quelle paire de caches rectangulaires (au moins de taille 2*2) (ou n'importe quelle famille de caches de hauteur fixée ou de largeur fixée). Avec 3 caches, je sais pas ce qui peut se passer.

[Patastronch]

Donc on ne peut pas obtenir un coloriage qui colorie seulement une case, donc a fortiori on ne peut pas obtenir tous les coloriages quelle que soit la grille.

Je suis pas convaincu par ce "a fortiori".
Dire qu'il est impossible de colorier un nombre impaire de cases en 1 coloriage, ca ne veut pas dire qu'avec une combinaison de coloriage on ne peut pas colorier un nombre impair de cases puisque l'intersection des coloriages peut etre impair.

Ou alors quelque chose m'a échappé ...

[Doraki]

Non, une combinaison de coloriages par caches 3*3 et 4*4 aura toujours un nombre de cases étoilées pair.

Si tu veux, par récurrence, quand tu choisis un cache 3*3 ou 4*4, ça va modifier un nombre pair de cases étoilées. Pour chacune de ces cases, elle est soit enlevée soit ajoutée au coloriage, et donc la parité du nombre de cases étoilées change. Puisqu'on fait un nombre pair de changements, au final, la parité ne peut pas être modifiée avec l'inversion d'un cache quel qu'il soit.

Si on considère la configuration qui contient 1 case noire et toutes les autres cases blanches, en plaçant le pavage de manière à ce que la case noire soit étoilée, la configuration contient alors un nombre de cases étoilées noires impair.
La configuration initiale contient 0 cases étoilées noires et 0 et 1 sont de parité différentes donc c'est impossible de passer d'une configuration toute blanche à une configuration avec 1 case noire, en coloriant avec les caches.

[Patastronch]

Oui en effet, c'est pas l'intersection qui doit être impair (j'ai dit une grosse bétise pardon!) mais la somme des changements effectués sur les cases étoilées. Et tu as mis en évidence que cette somme était paire quelque soit les combinaisons de coloriage.

Donc si tous coloriage A pouvait mener à un coloriage noir uni C, alors tous coloriages A pourraient être réduit à tout autre coloriage B par une suite de transformation (A->C->B) ,mais tu viens de montrer que c'était pas le cas.

Jolie démonstration !

[Doraki]

En fait, le coloriage est possible si et seulement si pour chacun de ces 24 pavages, le nombre de cases étoilées coloriées est pair.
(24 pavages parceque celui que j'ai montré peut être translaté horizontalement (*4), verticalement (*3) et peut être retourné en inversant les deux axes (*2))
Et en fait, seulement 12 pavages suffisent (ils ne sont pas linéairement indépendants).

Soit et dans (ce sont nos deux caches).

Il se trouve que 1+X+X² et 1+X+X²+X³ ( = (1+X)³) n'ont pas de facteurs communs, d'où il.. euh.. s'ensuit qu'on a la suite exacte de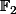 -espaces vectoriels :

(ça veut dire f injective, h surjective, Ker g = Im f, et surtout Ker h = Im g)

Où
où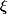 est une racine de 1+X+X², dans.

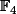L'application h' qui à un coloriage P associe les 12 valeurs obtenues avec les pavages est la même que h, à un changement de base de l'espace d'arrivée près.

Le fait que Ker h = Im g veut bien dire que les coloriages possibles (soit Im g) sont exactement ceux qui annulent h (la condition avec les pavages) (soit Ker h)

Pour la version graduée, les dimensions correspondantes obtenues sont pour une grille n×p, (avec n et p suffisemment grands),
0 -> (n-5)(p-5) -> (n-2)(p-2) + (n-3)(p-3) -> np -> 12 -> 0

(et on vérifie que (n-5)(p-5) + np = (n-2)(p-2) + (n-3)(p-3) + 12 = 2np + 5n + 5p + 25)

[Imod]

Je n'ai pas trop le temps ( ni le courage ) de lire tous ces messages pour le moment , mais ce n'est que partie remise :we:

Imod