Bonjour,
trouver tous les couples d'entiers naturels non nuls (a,b) qui vérifient la relation
a^(b²)=b^a
(les connaissances de Terminale S spé maths suffisent)
A^(b²)=b^a (pas très dur)
8 messages
- Page 1 sur 1
merci pour ce probleme Bizi

soit p un nombre premier qui divise a, alors p divise b
=aV_p(b))
donc=k\frac{a}{pgcd(a;b^2)} et V_p(b)=k\frac{b^2}{pgcd(a;b^2)})
avec K de IN*
alors il existe N de IN tel que:
}}) et
et }})
alors dans ce cas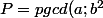=N^{\frac{min(a;2b^2)}{pgcd(a;b^2)}})
alors=b^2) si
si  sinon
sinon =a)
=> si
) avec
avec  est une solution et
est une solution et 
 on trouve facilement
on trouve facilement  ou
ou  ou
ou 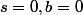 ou s=2;b=1 (s=2 pas une solution)
ou s=2;b=1 (s=2 pas une solution) 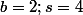 ou
ou 
si b>1 et s>4; (s=2 pas une solution)
(s=2 pas une solution)
,(0;0),(27;3),(16;2)})
=> si

 on trouve facilement a=0,t=0 ou a=1,t=1 et si a>1
on trouve facilement a=0,t=0 ou a=1,t=1 et si a>1 
S_2={(0;0),(1;1)}
S={(0;0),(1;1),(27;3),(16;2)}
NB: je ne suis pas sure de cette solution car je l'ai pas fait sur un bouillons
j'ecrit et je :marteau: ma tete en meme temp et a la fin j'ai posté sans verification et just apres :dodo:
soit p un nombre premier qui divise a, alors p divise b
donc
avec K de IN*
alors il existe N de IN tel que:
alors dans ce cas
alors
=> si
si b>1 et s>4;
=> si
S_2={(0;0),(1;1)}
S={(0;0),(1;1),(27;3),(16;2)}
NB: je ne suis pas sure de cette solution car je l'ai pas fait sur un bouillons
j'ecrit et je :marteau: ma tete en meme temp et a la fin j'ai posté sans verification et just apres :dodo:
puisque t'a trouvé ) alors ma solution est vrai
alors ma solution est vrai
par ce que j'ai trouvé que les solution s'ecrit sous la form
) ou
ou )
j'ai seulement fait une petite faute là:
=>
S={(0;0),(1;1),(27;3),(16;2)}
s'il existent d'autre solutions il faut qu'il verifie ce que j'ai trouvé dans ma 1er solution) ou
ou )
par ce que j'ai trouvé que les solution s'ecrit sous la form
j'ai seulement fait une petite faute là:
=>
j'ai pas vu s=b=3 et b=2;s=4
; b=0,s=1 ou b=1;s=1 ou b=0;s=0
S={(0;0),(1;1),(27;3),(16;2)}
s'il existent d'autre solutions il faut qu'il verifie ce que j'ai trouvé dans ma 1er solution
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
