montrez que si on a
Olympiades/exercice
11 messages
- Page 1 sur 1
olympiades/exercice
par kasmath » 30 Mai 2009, 11:44
salut
montrez que si on a
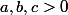
tel que 
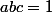
alors on obtienne :
}+\frac{2}{b^{5}(c^{3}+a^{3})}+\frac{2}{c^{5}(a^{3}+b^{3})}\ge 3)
montrez que si on a
par sniperamine » 30 Mai 2009, 13:33
on pose x=1/u y=1/v z= 1/r donc on aura
[u²/(v+r) + v²/(u+r) +r²/(v+u)]((v+r)+(u+r)+(u+v))>= ( u+v+r)² ( c'est l'inégalité de schwarz je crois)
et d'après l'inégalité aritho-geometrique (u+v+r)/2 >= 3/2(uvr)^(1/3)>=3/2
d'où 1/(x^3(y+z) + 1/(y^3(x+z) + 1/z^3(x+y) >= 3/2
maintenant si on pose a=x^(3/5) b=y^(3/5) c=z^(3/5) on aura l'inégalité demandée
donc j'ai utilisé 2 changements de variable pour trouver la solution
[u²/(v+r) + v²/(u+r) +r²/(v+u)]((v+r)+(u+r)+(u+v))>= ( u+v+r)² ( c'est l'inégalité de schwarz je crois)
et d'après l'inégalité aritho-geometrique (u+v+r)/2 >= 3/2(uvr)^(1/3)>=3/2
d'où 1/(x^3(y+z) + 1/(y^3(x+z) + 1/z^3(x+y) >= 3/2
maintenant si on pose a=x^(3/5) b=y^(3/5) c=z^(3/5) on aura l'inégalité demandée
donc j'ai utilisé 2 changements de variable pour trouver la solution
par sniperamine » 30 Mai 2009, 13:47
sniperamine a écrit:
maintenant si on pose a=x^(3/5) b=y^(3/5) c=z^(3/5) on aura l'inégalité demandée
donc j'ai utilisé 2 changements de variable pour trouver la solution
erf je me suis trompé ça donne pas y+z bon je réflechis après dsl
par sniperamine » 31 Mai 2009, 11:46
kasmath a écrit:ou est la réponse sa fait deux jours de travail sans :mur: ..
Je n'y ai pas réfléchi parce qu'apparemment tu cherches la réponse pour tes propres intérêts
par mohamed_idrissi7 » 01 Juin 2009, 01:46
d'aprés l'inégalité de la moyenne :
}+\frac{1}{b^5(a^3+c^3)}+ \frac{1}{c^5(a^3+b^3)} \ge 3(\frac{1}{(abc)^5(b^3+c^3)(a^3+c^3)(a^3+b^3)})^{1/3}=<br />3/2(\frac{2}{(b^3+c^3)}\frac{2}{(a^3+c^3)}\frac{2}{(b^3+c^3)})^{1/3})
Pour trouver l'inégalité demandée, il suffit de montrer que :
}\frac{2}{(a^3+c^3)}\frac{2}{(b^3+c^3)}\ge{1})
Or :
+ln(\frac{a^3+c3}{2})+ln(\frac{b^3+c3}{2})\ge ln(a^3)+ln(b^3)+ln(c^3) \ge 0)
(d'après l'inégalité de la convexité, et )
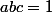
d'où le résultat!
Pour trouver l'inégalité demandée, il suffit de montrer que :
Or :
(d'après l'inégalité de la convexité, et
d'où le résultat!
par Zweig » 01 Juin 2009, 07:38
C'est faux, on a pas (c^3 + b^3)(a^3 + c^3) \leq 8)
En effet d'après l'inégalité arithmético-géométrique :(c^3 + b^3)(a^3 + c^3) \geq 2\sqrt{(ab)^3}\cdot2\sqrt{(bc)^3}\cdot 2\sqrt{(ac)^3} = 8(abc)^3 = 8)
En effet d'après l'inégalité arithmético-géométrique :
par mohamed_idrissi7 » 01 Juin 2009, 08:53
oui, c'est vrai! d'ailleur c'est ce que j'ai montré avec l'inégalité de convexité !!!! :zen:
dsl j'ai pas fait attention!
dsl j'ai pas fait attention!
par sniperamine » 01 Juin 2009, 12:35
mohamed_idrissi7 a écrit:oui, c'est vrai! d'ailleur c'est ce que j'ai montré avec l'inégalité de convexité !!!! :zen:
dsl j'ai pas fait attention!
Moi aussi j'avais pas fait attention en utilisant la 2éme variable
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :