Salut,
Je sais pas trop ce que tu attend comme réponse, mais ce genre d'isomorphisme, c'est une tautologie :
- Si tu part d'un élément de
)
et que tu compose (à gauche) par la projection canonique
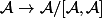
, tu obtient un élément de
)
qui est par construction nul sur les commutateurs, donc c'est une trace.
- Et réciproquement, si tu part d'un élément de
)
qui est une trace, alors il est (par définition d'une trace) nul sur tout les commutateurs donc (par linéarité) nul sur le s.e.v.
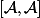
engendré par les commutateurs et ça signifie qu'il "passe au quotient", c'est à dire qu'il se factorise (à gauche) par la projection canonique
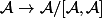
(c'est la définition en terme de diagramme commutatif de ce qu'est un "quotient" d'e.v. ou autres)