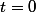
Zweig a écrit:En prenant, on obtient :
Désolé de revenir à la charge, mais ce passage m'est très flou :hein:
Inequality
22 messages
- Page 2 sur 2 - 1, 2
par Matt_01 » 10 Aoû 2008, 17:53
Désolé de revenir à la charge, mais ce passage m'est très flou :hein:
par acoustica » 10 Aoû 2008, 17:58
On peut le faire par Muirhead:
car (2,1,0) majore (1,1,1), ça marche aussi, non?
Effectivement, par Schur, c'est flou pour moi aussi.
Effectivement, par Schur, c'est flou pour moi aussi.
22 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :