F o f=exp
14 messages
- Page 1 sur 1
f o f=exp
Je vais imiter Nightmare et poser mes exos suivants ici, ils coulent trop vite dans le forum sup :
Donc voilà l'exercice est : montrer qu'il n'existe pas de fonction continue f sur C telle que f o f=exp.
Faisable avec outils terminale ( pour qui connait le théoreme des valeurs intermédiaires )
Donc voilà l'exercice est : montrer qu'il n'existe pas de fonction continue f sur C telle que f o f=exp.
Faisable avec outils terminale ( pour qui connait le théoreme des valeurs intermédiaires )
J'ai enfin la fin :
Comme={\bb C}^*) , il existe
, il existe  tels que
tels que =2i\pi) et
et =4i\pi) .
.
Comme=f(z)) on peut même choisir
on peut même choisir  et
et  tels que
tels que ) et
et ) soient dans
soient dans 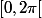 .
.
maizalors=f\circ f(b)=f(4i\pi)=f(2i\pi)=f\circ f(a)=\exp(a)) donc
donc  où
où  et compte tenu des hypothèses faites sur les parties imaginaires de
et compte tenu des hypothèses faites sur les parties imaginaires de  et
et  , on a forcément
, on a forcément 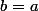 ce qui est légèrement en contradiction avec le fait que
ce qui est légèrement en contradiction avec le fait que \not= f(a)) !
!
Comme
Comme
maizalors
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est pour montrer que f(z+2i.pi)=f(z) :
1) foexp=fofof=expof
2) expof(z+2ipi)=foexp(z+2ipi)=foexp(z)=expof(z) donc f(z+2ipi)=f(z)+2k(z)ipi où k(z) est un entier qui, à priori, dépend de z
3) k(z)=[f(z+2ipi)-f(z)]/(2ipi) est une fonction continue (puisque f l'est) de C dans Z : elle est donc forcémént constante donc k(z)=k est indépendant de z.
4) de f(z+2ipi)=f(z)+2kipi on déduit (récurence) que, pour tout entier n,
f(z+2nipi)=f(z)+2knipi donc
exp(z)=exp(z+2ipi)=fof(z+2ipi)=f(f(z)+2kipi)=fof(z)+2k²ipi=exp(z)+2k²ip
ce qui montre que k=0.
1) foexp=fofof=expof
2) expof(z+2ipi)=foexp(z+2ipi)=foexp(z)=expof(z) donc f(z+2ipi)=f(z)+2k(z)ipi où k(z) est un entier qui, à priori, dépend de z
3) k(z)=[f(z+2ipi)-f(z)]/(2ipi) est une fonction continue (puisque f l'est) de C dans Z : elle est donc forcémént constante donc k(z)=k est indépendant de z.
4) de f(z+2ipi)=f(z)+2kipi on déduit (récurence) que, pour tout entier n,
f(z+2nipi)=f(z)+2knipi donc
exp(z)=exp(z+2ipi)=fof(z+2ipi)=f(f(z)+2kipi)=fof(z)+2k²ipi=exp(z)+2k²ip
ce qui montre que k=0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est quasiment ce que j'ai fait, bien joué ( comme d'hab^^). Petites remarques :
-de b=a+2ikpi, on en déduit f(a)=f(b) par ce que tu as fait avant, ce qui suffit pour conclure, donc c'est pas forcément la peine d'imposer de conditions pour que a=b
-à partir de f(z+2ipi)=f(z)+2ikpi, un autre moyen de prouver la nullitude de k et de de dire que f évite 0, et que donc cette relation implique que f évite 2ikpi, or f(C)=C*, donc nécéssairement k=0. Voilà c'est ni plus compliqué ni plus simple que ta méthode, mais c'est un autre moyen^^
Imod : sur R, de telles fonctions existent. Elles se construisent en gros en les définissant sur un intervalle de maniere a ce qu'elle vérifie certain trucs, puis en la prolongeant de proche en proche ( en gros le moyen classique de construire des solutions tordues a certaines equations fonctionnelles ). Et je crois bien d'ailleurs qu'on peut construire par ce procédé de telles fonctions C infinies. Reste le cas ou f est supposée localement analytique, qui est une question posée dans une rms. J'ai cherché un bon petit moment, mais je n'ai pas réussi à prouver qu'elles n'existent pas, ni à prouver qu'il y en a ( c'est que là, une construction "par morceaux" est à priori à proscrire )
-de b=a+2ikpi, on en déduit f(a)=f(b) par ce que tu as fait avant, ce qui suffit pour conclure, donc c'est pas forcément la peine d'imposer de conditions pour que a=b
-à partir de f(z+2ipi)=f(z)+2ikpi, un autre moyen de prouver la nullitude de k et de de dire que f évite 0, et que donc cette relation implique que f évite 2ikpi, or f(C)=C*, donc nécéssairement k=0. Voilà c'est ni plus compliqué ni plus simple que ta méthode, mais c'est un autre moyen^^
Imod : sur R, de telles fonctions existent. Elles se construisent en gros en les définissant sur un intervalle de maniere a ce qu'elle vérifie certain trucs, puis en la prolongeant de proche en proche ( en gros le moyen classique de construire des solutions tordues a certaines equations fonctionnelles ). Et je crois bien d'ailleurs qu'on peut construire par ce procédé de telles fonctions C infinies. Reste le cas ou f est supposée localement analytique, qui est une question posée dans une rms. J'ai cherché un bon petit moment, mais je n'ai pas réussi à prouver qu'elles n'existent pas, ni à prouver qu'il y en a ( c'est que là, une construction "par morceaux" est à priori à proscrire )
Ou l'image d'un connexe par une fonction continue est un connexe ,
Nike TN|TN Requin|Tn requin|Nike TN|Nike Ninja il sont costauds nos nouveaux Term S
Nike TN|TN Requin|Tn requin|Nike TN|Nike Ninja il sont costauds nos nouveaux Term S
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
