On dispose de la suite de chiffres visibles (il y a
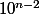
possibilités) et de la position des chiffres manquants (il y a
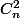
possibilités). On doit se débrouiller pour retrouver la suite totale de chiffres (il y a
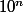
possibilités). Il faut
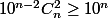
c'est à dire
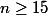
Refaisons la stratégie précédente pour vérifier que ça fonctionne pour
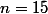
:
On découpe la suite par tranche de 2 chiffres en ajoutant un 0 à la fin puis on calcule modulo 100 la somme des nombres obtenus.
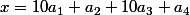
...mod 100. On numérote dans l'ordre lexicographique les paires possibles de chiffres à cacher et on cache justement la paire correspondant à

.
On peut déduire de la position des chiffres manquants la valeur de

et on peut calculer

comme

en remplaçant les chiffres cachés par 0, en calculant la différence entre
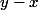
on trouve les opérations manquantes.
-si les chiffes cachés correspondent à sommer
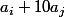
ou
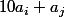
cela revient au cas précédent avec 2 chiffres adjacents et on peut identifier

et
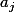
sans trop de difficultés
-si les chiffres cachés correspondent à sommer
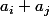
ou
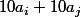
c'est moins bien car il y aura plusieurs couples possibles

Donc pour être sûre de moi, j'ai besoin de forcer un cache parmi les

et un cache parmi les
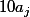
une idée facile serait de forcer un cache dans la première moitié et un cache dans la seconde moitié. Avec
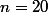
je devrais pouvoir m'en sortir puisque cela fait un découpage en 10+10 donc 10x10=100 possibilités pour les caches. Je calcule alors
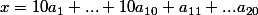
mais ce n'est pas optimisé donc on peut espérer mieux faire même si là je ne vois pas.
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.

