[Géométrie] Distance minimale
Olympiades mathématiques, énigmes et défis
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 19 Juin 2010, 13:41
par benekire2 » 19 Juin 2010, 13:41
Bonjour, petit problème de géométrie "olympique"
Soit (d) et (d') deux droites du plan non parallèles qui se coupent en I. On considère M un point strictement intérieur à l'angle formé par les deux droites, m et n des entiers naturels et
)
une droite passant par M. Cette droite coupe (d) en A et (d') en B.
Trouver la position de la droite
)
de sorte que le réel

soit minimal.
Bon travail.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 19 Juin 2010, 14:29
par Zweig » 19 Juin 2010, 14:29
Salut,
Sauf erreur, le minimum est obtenue lorsque la droite est telle que

. Il est clair qu'une telle droite est unique.
Soient K (IA) et L (IB) tels que (KM)//(IB) et (ML) // (IA). Dans ces conditions, on a :


Ainsi,
^m\cdot \left(\frac{AM}{AB}\right)^n})
Les points K et L ne dépendant pas de la droite, minorer cette expression revient à majorer le dénominateur. On pose

et

. Alors

et :
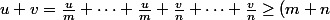\sqrt[m+n]{\frac{u^m}{m^m}\cdot \frac{v^n}{n^n}})
d'après AM-GM. D'où,
^{m+n}})
Le maximum est obtenu lorsque la condition plus haut est remplie.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 19 Juin 2010, 16:39
par benekire2 » 19 Juin 2010, 16:39
Je ne pouvais pas te l'apprendre, sachant que c'est un de tes posts d'un autre forum que j'ai jugé bon de remettre ici :id:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 19 Juin 2010, 16:44
par Zweig » 19 Juin 2010, 16:44
Oui, je me disais que j'avais déjà vu ce problème quelque part :we:.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités