Combinaison

par **Flyfsam** » 12 Aoû 2005, 21:07

Bonjour à tous je suis nouveau sur ce forum et pour tout vous dire, je suis nul en maths. Mais j'ai vais le pari avec un ami que je pouvait lui dire le nombre exacte de combinaison à 8 chiffres qu'il ya dans un tableau avec des chiffres allant de 1 à 20. Donc j'aimerai que vaut brillant cerveau m'aide à déchiffré le nombre de combinaison.
Merci d'avance à tous.

par **RadarX** » 12 Aoû 2005, 21:29

Flyfsam a écrit:Bonjour à tous je suis nouveau sur ce forum et pour tout vous dire, je suis nul en maths. Mais j'ai vais le pari avec un ami que je pouvait lui dire le nombre exacte de combinaison à 8 chiffres qu'il ya dans un tableau avec des chiffres allant de 1 à 20. Donc j'aimerai que vaut brillant cerveau m'aide à déchiffré le nombre de combinaison.
Merci d'avance à tous.

c'est qq chose de facile en fait et c'est connu = 125970 combinaisons si ma calculette ne me joue pas des tours!
Pour la formuule Cf tout litterature sur la proba ou surtout le denombrement!

Rx.

par **N_comme_Nul** » 12 Aoû 2005, 21:48

Salut !

Je trouve l'énoncé quelque peu ambigü.
On pourrait dire que c'est aussi

.
Ou bien encore

.

Et si l'on considérait que
[CENTER]1.12.3.4.5.6.7.8[/CENTER]
était la même "combinaison" que
[CENTER]11.2.3.4.5.6.7.8[/CENTER]
(il suffit de concaténer ...)

par **Flyfsam** » 12 Aoû 2005, 22:33

Merci les gars vous êtes vraiment trop fort. J'aimerai savoir si pour vous ça vous amuse de relevé des défis comme ça.

par **RadarX** » 13 Aoû 2005, 10:11

Moi personnellement, si j'ai du temps (ce qui n'est ps tjs le temps), alors oui, ca m'amuse. En fait c'est meme mieux, ca me sert aussi! En relevant des defis, on se rememore certaines choses qu'on regarde pas tout le temps ou bien ca fait faire des recherches et on apprend ainsi!
Tout donc , se resume a joindre l'utile a l'agreable!
Vla!
Rx.

par **Flyfsam** » 13 Aoû 2005, 17:36

Personnelement moi je n'arriverai jamais à relevé des défis comme toi.
Et je me demande, mais ça doit être impossible de calculer combien il y a de combinaison sur les 125 970 qui contiennent que des chiffres paires et celles ou il y a que des chiffrs impaires.

par **N_comme_Nul** » 13 Aoû 2005, 18:15

Salut !

Chiffres ou nombres ? (ça fait deux problèmes)

par **Galt** » 13 Aoû 2005, 18:26

Avec 8 chiffres parmi 20, si on tient compte de l'ordre il y a 20*19*18*17*16*15*14*13 combinaisons, ce qui fait 5079110400 possibilités de combinaisons (j'ai 20 manières de choisir le premier nombre, 19 de choisir le deuxième et ainsi de suite, 13 manières de choisir le 8ème chifre). Le nombre 125970 s'obtient si on ne tient pas compte de l'ordre, c'est à dire si on considère que la combinaison 1 2 3 4 5 6 7 8 est la même que 8 7 5 6 3 4 1 2 ou que 8 3 4 7 5 1 6 2 (etc, il y a 40320 manières d'ordoner ces 8 chifres)
Il y a en tout 10 nombres pairs, donc 10*9*8*7*6*5*4*3 possibilités de combinaisons (si on tient compte de l'ordre), ce qui en fait 1814400, et autant avec seulement des nombres impairs. Si on ne tient pas compte de l'ordre, il reste 45 possibilités avec les nombres pairs seuls (et aussi 45 avec les nobres impairs seuls)
Le total ne fait bien sûr pas 125970 puisque la plupart des combinaisons contiennent à la fois des nombres pairs et des nombres impairs
Galt

par **LEX** » 13 Aoû 2005, 18:56

Galt a écrit:Avec 8 chiffres parmi 20, si on tient compte de l'ordre il y a 20*19*18*17*16*15*14*13 combinaisons, ce qui fait 5079110400 possibilités de combinaisons (j'ai 20 manières de choisir le premier nombre, 19 de choisir le deuxième et ainsi de suite, 13 manières de choisir le 8ème chifre).

Oui mais la c'est si tu fais sans répétition... En effet, tu pourrais placer 2 fois le chiffre 18 par exemple.
8 chiffres, chacun des chiffres allant de 1 a 20 et non pas parmi 20.

Exemple : 1, 2, 1, 3, 5, 20, 28, 17, 17 ... Enfin c'est comme ca que j'avais compris. (Ca ferait alors 20^8 si c'est avec ordre et avec répétition).

par **Flyfsam** » 13 Aoû 2005, 19:19

Là vraiment vous m' impréssioné. Et est ce que vous seriez capable de savoir combien il y a de combinaison de 8 chiffre allant de 1 à 8 parmi 20 numéros mais en enlevant toutes les combinaison ayant 5 6 7 et 8 chiffres qui se suivent.(ex : 1.3.6.7.8.9.10.11). Et la mon ami sera bluffé.

par **Galt** » 14 Aoû 2005, 11:08

Ca se corse
Je vais faire le calcul sans tenir compte de l'ordre
Des combinaisons avec les 8 chiffres qui se suivent, il y en a 13 (de 12345678 à 13 14 15 16 17 18 19 20)
Avec 7 chiffres qui se suivent, il y en a bien sûr 14. Je dois les compléter par un nombre, et j'ai en général 11 choix (j'ai utilisé 7 nombres, il en reste 13 mais je ne peux pas prendre les extrêmités), sauf pour les combinaisons 1 2 3 4 5 6 7 et 14 15 16 17 18 19 20 où il n'y a qu'une extrêmité (et donc 12 choix disponibles pour le 8 ème chiffre), soit 12*11 + 12*2 = 12*13 = 156 possibilités.
Avec 6 chiffres qui se suivent, 15 combinaisons. On doit les compléter par 2 chiffres, il y en a 12 disponibles pour 13 d'entre elles, ce qui done 66 choix de 2 chiffres, et 13 disponibles pour les deux dernières, soit 78 possibilités de 2 chiffres. Finalement 13*66+2*78 = 13*(66+24) = 13*90=1170 possibilités
Et enfin avec 5 chiffres (même méthode) : 14*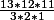

+ 2*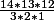

, soit 4732 possibilités, sauf erreur
Au total : 4732+1170+132+13=6047 possibilités, et il ne reste plus qu'une soustraction.

par **Galt** » 14 Aoû 2005, 11:10

Je remarque dans mon calcul précédent que pour chaque étape j'obtiens un multiple de 13.
Quelqu'un a-t-il une idée pour une méthode de calcul plus simple qui ferait apparaître ces facteurs 13 de manière éclatante ?
Galt

par **scelerat** » 17 Aoû 2005, 13:15

Galt a écrit:Je remarque dans mon calcul précédent que pour chaque étape j'obtiens un multiple de 13.
Quelqu'un a-t-il une idée pour une méthode de calcul plus simple qui ferait apparaître ces facteurs 13 de manière éclatante ?
Galt

Comme tu le dis, et que je l'ai repris dans une autre discussion, le nombre de
de combinaisons de p parmi n avec q consecutifs est

Ca peut aussi s'ecrire, en reduisant au meme denominateur,

On a donc (n-p+1) en facteur, quelle que soit la valeur de q.
20-8+1 = 13, CQFD.

par **mcrafi** » 20 Aoû 2005, 18:12

Salut,
j'ai une idée à ajouter...
la combinaison de 8 elements(chiffres ou nombres) parmi 20.
[CENTER]8[/CENTER]
[CENTER]=C [/CENTER] [/CENTER] [CENTER]20[/CENTER]
Bah c'est ça je crois.
et bien tout simplement c'est egale à = 20!/(20-8)!*8!=125970

Qu'en pensent les autres?

Combinaison

Combinaison

Qui est en ligne