3 => chaos

par **windows7** » 08 Juil 2010, 09:05

salut

soit f continue de [0,1] dans [0,1].
montrer que si f admet un point de periode 3, alors elle admet des points de toutes periodes

par **Ben314** » 08 Juil 2010, 09:47

Je passe mon tour (je connais). Pour ceux qui veulent aller plus loin :
Montrer que la relation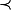

définie sur

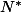par :

Toute fonction continue f:[0,1]->[0,1] admettant un point de période n admet forcément un point de période m.
est une relation d'ordre totale sur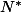

et la décrire.

(La question de window7 revient à montrer que 3 est le plus petit élément de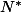

pour la relation

)

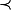Quelques précisions :
- Un point x de [0,1] et dit "point de période n" lorsque c'est un point fixe de

(n fois) et que ce n'est pas un point fixe de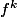

pour un k<n.
- La preuve est un peu astucieuse mais ne demande quasi aucune connaissances...

par **windows7** » 08 Juil 2010, 09:52

salut ben

oui c'est bien ca :zen:

( pour revenir sujet plus ou moin confus " une suite periodique " dans la rubrique olympiade, c'est a ce theoreme que je faisais reference, sans toutefois avoir verifié qu'on pouvait l'utiliser )

par **Nightmare** » 08 Juil 2010, 12:11

Joli :happy3: Pas difficile quand on a "vu" ce qu'il se passait.

par **Ben314** » 08 Juil 2010, 12:29

windows7 a écrit:salut ben

oui c'est bien ca :zen:

( pour revenir sujet plus ou moin confus " une suite periodique " dans la rubrique olympiade, c'est a ce theoreme que je faisais reference, sans toutefois avoir verifié qu'on pouvait l'utiliser )

Si je me rapelle bien la preuve du résultat, il suffit que f soit continue de I->I où I est un intervalle pas nécéssairement fermé pour que ça marche.

Le problème avec la méthode de Newton, c'est que, si la fonction de départ f admet quelque part une tangente horizontale alors la fonction un->u(n+1) n'est pas définie en ce point et cela fait un "trou" dans le domaine de définition. En prenant les images réciproques du "trou", ça risque de faire beaucoup de "trous".

Un exemple (à la con, mais rigolo) :
On considère les suites correspondant à la méthode de Newton associée à f(x)=x²+1 : on a donc U(n+1)=Un-f(Un)/f'(Un)=(Un²-1)/(2Un).
Question 1 : Quel est l'ensemble des valeurs initiales Uo pour lesquelle la suite Un est défini pour tout entier n ?
Question 2 : Pours quels entiers p existe t'il des points de période p ? Combien y-a-t'il de tels points ?
Par exemple, ici, vu le résultat de la question 1, tu risque pas d'appliquer le fameux théorème pour répondre à la question 2 vu que...

par **Ben314** » 08 Juil 2010, 12:33

Nightmare a écrit:Joli :happy3: Pas difficile quand on a "vu" ce qu'il se passait.

Tu as trouvé la relation d'ordre ou seulement montré que 3 est le plus petit élément ?

par **windows7** » 08 Juil 2010, 12:39

j'ai une vision sado masochiste : ca me fait penser a des coups de fouet ! enfin je me comprend :zen:

par **benekire2** » 08 Juil 2010, 18:47

Salut,
l'énoncé initial m'a pas l'air évident [du moins pour moi...]

Le seul "théorème" que je conaisse concernant les points fixes est que si un intervalle I est inclus dans son image alors il y a au moins un point fixe ( application continue évidemment )

Ceci dit mon "idée" est de construire les points fixes de f^k via ce théorème et par récurrence sur k ...

Est-ce qu'il faut procéder dans ce "genre" ?

par **ffpower** » 08 Juil 2010, 21:12

Précisément, oui :we:

par **Finrod** » 08 Juil 2010, 21:12

Je connais aussi mais je n'ai jamais regardé la preuve.

Il y a un ordre donné ici [url]http://fr.wikipedia.org/wiki/Théorème_de_Sarkovskii[/url] qui est différent du tiens Ben.

Je n'aurais rien contre un indice sur la méthode.

edit : Je viens de voir une preuve avec google. C'est suffisamment long pour que je n'ai pas le temps de le lire ! Pour le moment en tout cas.

par **Ben314** » 08 Juil 2010, 22:46

Finrod a écrit:Il y a un ordre donné ici [url]http://fr.wikipedia.org/wiki/Théorème_de_Sarkovskii[/url] qui est différent du tiens Ben.

Heuuuu, tu peut m'expliquer en quoi il est différent du mien ?

par **Ben314** » 08 Juil 2010, 22:51

benekire2 a écrit:...si un intervalle I est inclus dans son image alors il y a au moins un point fixe ( application continue évidemment )...

Fait gaffe, c'est faux si I n'est pas un intervalle fermé borné :
par exemple x->x^2 de I=]0,1[ dans lui même n'a pas de point fixe
et x->x+1 de I=R dans lui même non plus...
Pour cet exo. le seul "prérequis" est le théorème des valeurs intermédiaires

par **Finrod** » 09 Juil 2010, 07:34

Ben314 a écrit:Heuuuu, tu peut m'expliquer en quoi il est différent du mien ?

En effet, je t'avais mal lu. dsl.

par **benekire2** » 09 Juil 2010, 07:47

Re !

Bah, après avoir cherché un peu plus, je vois pas comment commencer ... quelqu'un pourrait-il me donner le début s'il vous plait ?

Merci :id:

par **Finrod** » 09 Juil 2010, 07:51

Il faut regarder les points a, f(a) et f²(a) quand a est 3-périodique.

(Aller Je vais essayer aussi de retrouver l'idée de la preuve)

aaaah ça y est j'ai compris l'argument. Je savais qu'il fallait trouver deux points tels que f(x1)x2, je me doutais qu'ils étaient parmi les 3 points cités ci-dessus.

Allez savoir pourquoi j'avais pas vérifier pour f(a) et f²(a) jusqu'à maintenant...

par **benekire2** » 10 Juil 2010, 09:43

Salut Finrod, en fait je vois pas trop comment faire avec ce que tu dit et pour trouver tes x1 et x2 tels que f(x1)x2 ...

par **mt2sr** » 10 Juil 2010, 11:58

a, f(a), f²(a) sont diff on peut supposer que a

3 => chaos

3 => chaos

Qui est en ligne