Calcul de limite (pas très dur)

par **nekros** » 18 Juil 2006, 00:01

salut,
Soit

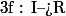
de classe

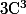
sur I.

Calculer

Bonne chance.

Thomas G :zen:

par **Nightmare** » 18 Juil 2006, 00:38

Bonsoir :happy3:

On pose g(x)=f(a+3x)-3f(a+2x)+3f(a+x)
g(0)=f(a) donc la limite recherchée est équivalente à

En utilisant 3 fois la règle de l'hospital cette limite vaut :

On a :
g'(x)=3f'(a+3x)-6f'(a+2x)+3f'(a+x)
g''(x)=6f''(a+3x)-12f''(a+2x)+3f''(a+x)
g'''(x)=18f'''(a+3x)-24f'''(a+2x)+3f'''(a+x)

donc g'''(0)=-3f'''(a)

Ainsi la limite recherchée est

:happy3:

par **Sdec25** » 18 Juil 2006, 00:43

Salut

La limite est la dérivée 3ième.

par **Nightmare** » 18 Juil 2006, 00:46

Ouch je ne sais même plus faire une multiplication ...

g'''(x)=27f'''(a+3x)-24f'''(a+2x)+3f'''(a+x) bien sûr

par **Nightmare** » 18 Juil 2006, 00:46

donc la limite vaut bien 6f'''(a)/6=f'''(a)

par **nekros** » 18 Juil 2006, 01:01

Bravo à vous deux :we:

On pouvait aussi tout simplement utiliser la formule de Taylor-Young.

est de classe

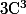
donc :

Donc

Merci d'avoir participé !

Thomas G :zen:

par **Nightmare** » 18 Juil 2006, 01:04

Au passage, ma solution est bonne si f est C^3 mais dans ton énoncé tu ne précises pas que la dérivée 3éme est continue...

par **nekros** » 18 Juil 2006, 01:09

f est de classe C^3 signifie que f est trois fois dérivable et que la dérivée troisième est continue.
Où est le problème ? :hein:

Thomas G :zen:

par **Nightmare** » 18 Juil 2006, 01:10

Oui mais dans le post initial tu indiques seulement que f est trois fois dérivable et non qu'elle est de classe C3 :happy3:

par **nekros** » 18 Juil 2006, 01:13

:ptdr: exact ! encore un oubli :marteau:
C'est corrigé.

Thomas G :zen:

par **nekros** » 18 Juil 2006, 01:15

Sinon, concrètement, c'est quoi la règle de l'Hospital : jamais vu ça :hein: :hein:

Thomas G :zen:

par **Nightmare** » 18 Juil 2006, 01:21

Voir ici

:happy3:

par **nekros** » 18 Juil 2006, 01:23

Ok merci :++:

Thomas G :zen:

par **Nightmare** » 18 Juil 2006, 01:24

De rien :happy3:

Sur ce je vais me coucher. A demain peut être pour de nouveaux calculs :lol3:

par **nekros** » 18 Juil 2006, 01:42

Bonne nuit !

Thomas G :zen:

Calcul de limite (pas très dur)

Calcul de limite (pas très dur)

Qui est en ligne