Baguette tournante

[Imod]

Bonjour à tous

Une question que j'ai déjà posée ailleurs et qui pourrait intéresser certains membres du forum :

On considère un polygone simple du plan et une baguette rectiligne dont les extrémités sont liées à la frontière du polygone . La baguette est de taille maximale dans le sens où lorsqu’elle se déplace , ses extrémités peuvent couvrir le périmètre du polygone alors que ce serait impossible avec une baguette plus grande .

La question : dans cette situation , une des extrémités de la baguette est-elle assurée de pouvoir parcourir la totalité du périmètre ?

Merci d'avance pour la participation

Imod

[LeJeu]

Bonjour Imod,

J'ai lu ta question avec intérêt , et le matin au café je fais tourner une allumette sur différentes figures !
Et avant de te répondre, j'ai bien lu, pour ne pas être hors jeu les propositions, sur le site ami , Une baguette

Ton énoncé étant assez confusionnant, je l’interprète comme " Quelle est la taille maximum de la baguette, telle que les deux extrémités puissent faire faire le tour du polygone"

J'ai donc lu le cas du triangle équilatéral où la taille maxi est la hauteur,
et celui du rectangle ou la taille maxi est le 'petit coté,

Je suis donc passé tranquillement au quadrilatère convexe, ( je sais , c'est un peu trivial)

et " on voit" assez vite que la baguette doit dans certains cas "se retourner" , en gros : la tête arrive dans un angle aigu, et pour pouvoir continuer , la queue doit reculer, ok , mais pour pouvoir progresser , il faut arriver au moment où, la tête progressant, la queue reculant, la baguette puisse se "retourner" et qu'alors la tête se mette à reculer jusqu'à ce que la queue de la baguette arrive à l'angle en question !

Ci dessous je fais tourner la tête ( O) autour du quadrilatère, et indique les marches avant /arrière nécessaires, et les deux retournements ( en vert)




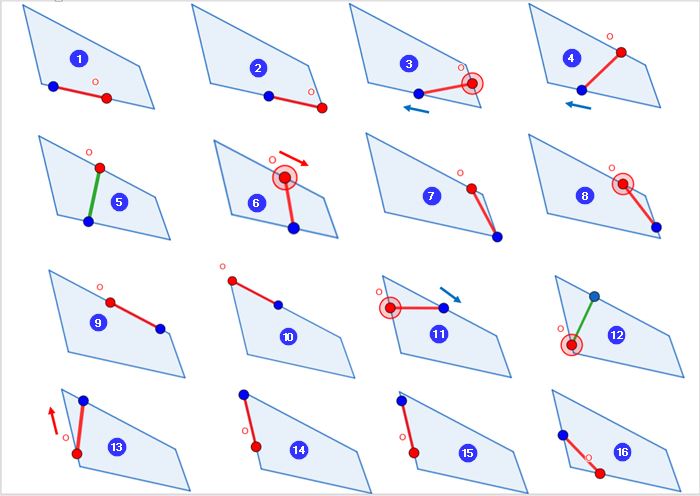
Dans cet exemple la taille maximum se trouve sur le retournement de la vignette 12, et nous est donnée par la longueur de la perpendiculaire



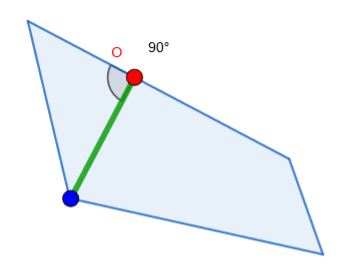
Ce qui est cohérent avec les cas particuliers du triangle et du rectangle

[beagle]

Un petit bonjour nostalgique aux anciens,
Dominique et ses fameux "petits problèmes",
LeJeu le bon temps où on pouvait s'amuser en faisant des maths !

[beagle]

Marrant, LeJeu est-il faché depuis notre dernier fil de discussion ?

[Imod]

Merci pour vos réponses

Il s'agit d'un problème que j'ai en tête depuis un moment et il peut se décliner en de nombreuses variantes toutes plus intéressantes les unes que les autres . J'ai essayé de proposer une classification des questions sur le site évoqué par LeJeu mais elle n'est vraiment pas satisfaisante .

La question que j'ai posté ici est mal posée car on peut l'interpréter de plusieurs façons . Dans le cas d'un polygone convexe la réponse au tour complet semble être donnée par la largeur de la plus petite bande enfermant le polygone ( il n'y a pas plus de bandes intéressantes que de côtés ) .

Une question "simple" qui reste ouverte : une extrémité de la baguette peut parcourir tout le périmètre du polygone , en est-il toujours de même pour l'autre ?

Imod

PS : j'ai aussi proposé une version du problème sur l'île des maths et Verdurin a proposé une variante .