Le point sur l'hypothèse de Riemann
16 messages
- Page 1 sur 1
Le point sur l'hypothèse de Riemann
Bonsoir,
Par curiosité plus qu'autre chose j'aimerais faire un point sur l'hypothèse de Riemann sachant que :
- Elle n'a jamais été mise en défaut à l'aide d'un contre exemple
- Elle a été "conforté" par le calcul de plus d'un milliard de zéros situés sur la droite
- Il à été démontré qu'au moins 40% des zéros se trouvaient sur cette droite
Y a t il du nouveau depuis tout ça ?
Pourquoi n'admettons pas cette hypothèse comme vraie vu qu'elle semble indestructible (et en même temps non prouvable et c'est la que ça devient agaçant) ?
En même temps qu'est ce que ça impliquerait si l'hypothèse de Riemann était tenue pour vraie ?
A mon simple niveau, je me dis que cela permettrait tout au plus de définir plus finement la quantité de nombres premiers inférieurs à une certaine valeur ... ne serait ce donc la le seul intérêt ?
Par curiosité plus qu'autre chose j'aimerais faire un point sur l'hypothèse de Riemann sachant que :
- Elle n'a jamais été mise en défaut à l'aide d'un contre exemple
- Elle a été "conforté" par le calcul de plus d'un milliard de zéros situés sur la droite
- Il à été démontré qu'au moins 40% des zéros se trouvaient sur cette droite
Y a t il du nouveau depuis tout ça ?
Pourquoi n'admettons pas cette hypothèse comme vraie vu qu'elle semble indestructible (et en même temps non prouvable et c'est la que ça devient agaçant) ?
En même temps qu'est ce que ça impliquerait si l'hypothèse de Riemann était tenue pour vraie ?
A mon simple niveau, je me dis que cela permettrait tout au plus de définir plus finement la quantité de nombres premiers inférieurs à une certaine valeur ... ne serait ce donc la le seul intérêt ?
Re: Le point sur l'hypothèse de Riemann
Je ne suis absolument pas un spécialiste mais je pense pouvoir te répondre sur notamment ta question de : pourquoi ne pas admettre que c'est vrai.
Et la réponse est très simple : il existe des résultats mathématiques qui ne sont vrais que jusqu'à certaines valeurs (même très grandes) et tester jusqu'à des grands nombres ne vaut pas grand-chose en mathématiques si ce n'est se faire une idée du résultat.
On construit les mathématiques sur des démonstrations : comment aurais-tu réagi si on t'avais dis en 4° "vous pouvez utiliser le théorème de Pythagore, on n'est pas sûr qu'il est juste, mais ça a l'air d'être le cas".
On ne peut pas construire les maths sur des intuitions, des "je pense que", des "je suis quasi-sûr que" car sinon on arrêterait pas d'avoir faux, un sacrilège en maths !! Bref, il faut démontrer.
Et (très) rapidement, connaître la répartition des nombres premiers serait déjà une IMMENSE avancée car ce serait la première fois à ma connaissance (me corriger si c'est faux) que l'on relierait analyse et arithmétique.
Et la réponse est très simple : il existe des résultats mathématiques qui ne sont vrais que jusqu'à certaines valeurs (même très grandes) et tester jusqu'à des grands nombres ne vaut pas grand-chose en mathématiques si ce n'est se faire une idée du résultat.
On construit les mathématiques sur des démonstrations : comment aurais-tu réagi si on t'avais dis en 4° "vous pouvez utiliser le théorème de Pythagore, on n'est pas sûr qu'il est juste, mais ça a l'air d'être le cas".
On ne peut pas construire les maths sur des intuitions, des "je pense que", des "je suis quasi-sûr que" car sinon on arrêterait pas d'avoir faux, un sacrilège en maths !! Bref, il faut démontrer.
Et (très) rapidement, connaître la répartition des nombres premiers serait déjà une IMMENSE avancée car ce serait la première fois à ma connaissance (me corriger si c'est faux) que l'on relierait analyse et arithmétique.
Re: Le point sur l'hypothèse de Riemann
Bof, on la connait déjà la répartition des nombres premiers (cf. le théorème des nombres premiers). Concernant la jonction analyse/arithmétique, elle existe déjà et ça ne date pas d'hier (cf la relation d'Euler) sans compter que la fonction zeta n'est pas la seule qui pourrait lier analyse et arithmétique. Alors la démonstration de l'hypothèse de Riemann amènerait quoi ?
Re: Le point sur l'hypothèse de Riemann
Le théorème des nombres premiers ne dit pas tout sur la répartition des nombres premiers. Il donne une info dessus, et en supposant que HR soit vraie, on a une meilleure info dessus.
Après, comme pour la plupart des problèmes de maths pures, si on s'intéresse à HR c'est pas tant pour son énoncé en lui-même, mais plutôt parce que la résoudre (ie réussir à démontrer qu'elle est vraie/fausse/indécidable) serait une étape importante dans l'avancée des maths en général. C'est en quelque sorte un but symbolique à atteindre. D'ailleurs, on s'en fout un peu qu'elle soit vraie ou fausse, mais il y a fort à parier qu'une démonstration nécessite de développer de nouveaux outils et techniques qui ouvriront tout un champ de possibilités et applications nouvelles (cf le grand théorème de Fermat, qui est un théorème quasi-inutile en lui-même).
Après, comme pour la plupart des problèmes de maths pures, si on s'intéresse à HR c'est pas tant pour son énoncé en lui-même, mais plutôt parce que la résoudre (ie réussir à démontrer qu'elle est vraie/fausse/indécidable) serait une étape importante dans l'avancée des maths en général. C'est en quelque sorte un but symbolique à atteindre. D'ailleurs, on s'en fout un peu qu'elle soit vraie ou fausse, mais il y a fort à parier qu'une démonstration nécessite de développer de nouveaux outils et techniques qui ouvriront tout un champ de possibilités et applications nouvelles (cf le grand théorème de Fermat, qui est un théorème quasi-inutile en lui-même).
Re: Le point sur l'hypothèse de Riemann
Attention tout de même avec ce type de raisonnement car de mémoire il me semble que le théorème des nombres premiers a été démontré avec des outils d'analyse standard la ou beaucoup de matheux (Hardy et sa bande en première ligne) s'attendait à voir une démonstration ayant recours à de l'analyse dite complexe alors que...
On ne peut pas parier aveuglément sur de nouveaux outils sous prétexte que le temps passe et que personne n'y parvienne. En même temps, je me dis que compte tenu des techniques et du panel de matheux exerçant aujourd'hui, ça semble étrange que l'hypothèse n'ait pas été infirmée (ou démontrée) !
Mais j'en reviens à la question, quand bien même un scientifique parvienne à démontrer l'hypothèse qu'est ce que ça changerait ?
On ne peut pas parier aveuglément sur de nouveaux outils sous prétexte que le temps passe et que personne n'y parvienne. En même temps, je me dis que compte tenu des techniques et du panel de matheux exerçant aujourd'hui, ça semble étrange que l'hypothèse n'ait pas été infirmée (ou démontrée) !
Mais j'en reviens à la question, quand bien même un scientifique parvienne à démontrer l'hypothèse qu'est ce que ça changerait ?
Re: Le point sur l'hypothèse de Riemann
Bonsoir,
Vu qu'il y a beaucoup de recherches aujourd'hui qui prennent cette hypothèse pour point de départ, on peut dire qu'en pratique elle est considérée comme vraie... Mais théoriquement, elle n'est pas vraie tant qu'elle n'est pas rigoureusement démontrée, un point c'est tout, puisque sans démonstrations rigoureuses les mathématiques perdraient leur raison d'être.
Ici un petit aperçu en anglais des conséquences de l'HR :
http://mathoverflow.net/questions/17209/consequences-of-the-riemann-hypothesis
voir par exemple le point e) sur la conjecture de Goldbach.
Un autre point intéressant : j'entendais C. Villani dire que les zéros de la fonction zeta étaient peut-être reliés à des niveaux d'énergie en mécanique quantique, ou aux spectres de certains opérateurs sur certains espaces de Hilbert (cf http://iml.univ-mrs.fr/editions/publi2005/LaRechercheHS20_Lachaud.pdf)... Quelqu'un peut-il nous dire ce qu'il en est de cette piste aujourd'hui ?
anthony_unac a écrit:Pourquoi n'admettons pas cette hypothèse comme vraie vu qu'elle semble indestructible (et en même temps non prouvable et c'est la que ça devient agaçant) ?
En même temps qu'est ce que ça impliquerait si l'hypothèse de Riemann était tenue pour vraie ?
Vu qu'il y a beaucoup de recherches aujourd'hui qui prennent cette hypothèse pour point de départ, on peut dire qu'en pratique elle est considérée comme vraie... Mais théoriquement, elle n'est pas vraie tant qu'elle n'est pas rigoureusement démontrée, un point c'est tout, puisque sans démonstrations rigoureuses les mathématiques perdraient leur raison d'être.
Ici un petit aperçu en anglais des conséquences de l'HR :
http://mathoverflow.net/questions/17209/consequences-of-the-riemann-hypothesis
voir par exemple le point e) sur la conjecture de Goldbach.
Un autre point intéressant : j'entendais C. Villani dire que les zéros de la fonction zeta étaient peut-être reliés à des niveaux d'énergie en mécanique quantique, ou aux spectres de certains opérateurs sur certains espaces de Hilbert (cf http://iml.univ-mrs.fr/editions/publi2005/LaRechercheHS20_Lachaud.pdf)... Quelqu'un peut-il nous dire ce qu'il en est de cette piste aujourd'hui ?
Re: Le point sur l'hypothèse de Riemann
Faut il comprendre que si l'hypothèse est vraie alors la conjecture de Goldbach l'est également ?
Mais quand bien même, en quoi cela nous avance t il de savoir que la conjoncture de Goldbach est vraie ? C'est du même acabit que HR ?
Mais quand bien même, en quoi cela nous avance t il de savoir que la conjoncture de Goldbach est vraie ? C'est du même acabit que HR ?
Re: Le point sur l'hypothèse de Riemann
Oui, mais il est précisé qu'il s'agit seulement de la conjecture impaire ou "odd" (tout nombre impair supérieur à 7 est somme de trois nombres premiers), qui est plus faible que la conjecture classique, et qui a été démontrée complètement en 2013. Enfin du coup c'était juste un exemple un peu différent du thm des nombres premiers...
A quoi ça sert ? et bien déjà à s'endormir moins bête le soir, comme l'a déjà dit Skullkid sous une forme plus poétique, et en ce qui me concerne, cela est déjà bien suffisant.
A quoi ça sert ? et bien déjà à s'endormir moins bête le soir, comme l'a déjà dit Skullkid sous une forme plus poétique, et en ce qui me concerne, cela est déjà bien suffisant.

Re: Le point sur l'hypothèse de Riemann
S'il suffisait de compter "très loin" pour que ça marche on serait embêter. Y a des conjectures qui se révèlent fausses après très longtemps alors qu'on croyait qu'elles étaient vraies ; grâce à l'outil informatique ou un petit génie très habile. Par exemple on a la conjecture d'Euler (" "grand théorème de Fermat généralisé" ").
Tenez pour enfoncer le couteau un peu plus loin: les deux conjectures de Hardy Littlewood. Aucune n'est vérifiée et on pense que l'une est fausse! On estime le premier contre exemple à environ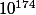 cf https://sciencetonnante.wordpress.com/2014/10/13/deuxieme-conjecture-hardy-littlewood/.
cf https://sciencetonnante.wordpress.com/2014/10/13/deuxieme-conjecture-hardy-littlewood/.
Qu'est ce qui nous dit que la conjecture Zhéta de Riemann n'a pas de zéro de module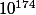 et de partie réelle différente de 1/2? Parce qu'on a essayé très loin? Très loin c'est subjectif et ça dépend essentiellement de l'époque à laquelle on se trouve. Je suis sûr qu'Euler avait calculer "très loin" pour son époque avant d'émettre sa conjecture. Bon, parce que les gens qui pensent que c'est vrai sont très intelligents? Bin Euler était pas idiot non plus. Et le bon sens aussi dépend de l'époque, avant
et de partie réelle différente de 1/2? Parce qu'on a essayé très loin? Très loin c'est subjectif et ça dépend essentiellement de l'époque à laquelle on se trouve. Je suis sûr qu'Euler avait calculer "très loin" pour son époque avant d'émettre sa conjecture. Bon, parce que les gens qui pensent que c'est vrai sont très intelligents? Bin Euler était pas idiot non plus. Et le bon sens aussi dépend de l'époque, avant  tous les mathématiciens (certes il n'y avait pas foule) pensaient que tous les nombres étaient rationnels. Parce qu'on veut que ce soit vrai? C'est pour moi le seul argument et il est pas très recevable...
tous les mathématiciens (certes il n'y avait pas foule) pensaient que tous les nombres étaient rationnels. Parce qu'on veut que ce soit vrai? C'est pour moi le seul argument et il est pas très recevable...
Les nombres astronomiques sont vraiment inimaginables pour nous. Rien que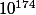 on pourrait pas l'écrire en transformant toute la matière de l'univers en encre... Par exemple le plus gros groupe sporadique qui existe a juste 808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 éléments, sporadique veut dire qu'il ressemble pas trop aux autres, qui aurait pu imaginer qu'il y en aurait juste 26 (ou 27) comme ça...
on pourrait pas l'écrire en transformant toute la matière de l'univers en encre... Par exemple le plus gros groupe sporadique qui existe a juste 808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 éléments, sporadique veut dire qu'il ressemble pas trop aux autres, qui aurait pu imaginer qu'il y en aurait juste 26 (ou 27) comme ça...
Bref, les mathématiques sont pleines de surprises et je suis sûr que la communauté mathématiques aura encore plein de grosses désillusions et de belles démonstrations très attendues. L'intuition nous guide mais ça peut être notre pire ennemi . Et dans tout ça rien n'empêche d'avoir son avis bien sûr et le mien aussi est que la conjecture de Riemann est vraie mais ça a à peu près autant de valeur qu'un aveugle qui donne la météo de 2048
. Et dans tout ça rien n'empêche d'avoir son avis bien sûr et le mien aussi est que la conjecture de Riemann est vraie mais ça a à peu près autant de valeur qu'un aveugle qui donne la météo de 2048 
Tenez pour enfoncer le couteau un peu plus loin: les deux conjectures de Hardy Littlewood. Aucune n'est vérifiée et on pense que l'une est fausse! On estime le premier contre exemple à environ
Qu'est ce qui nous dit que la conjecture Zhéta de Riemann n'a pas de zéro de module
Les nombres astronomiques sont vraiment inimaginables pour nous. Rien que
Bref, les mathématiques sont pleines de surprises et je suis sûr que la communauté mathématiques aura encore plein de grosses désillusions et de belles démonstrations très attendues. L'intuition nous guide mais ça peut être notre pire ennemi
Re: Le point sur l'hypothèse de Riemann
D'après le livre de JP Delahaye "Le fascinant nombre pi", le nombre défini par
^2)
est une approximation de pi qui a plus de 42 milliards de décimales exactes. Si l'on avait du rendre un jugement seulement sur la base de quelques millions de décimales, on se serait salement trompés... il convient donc de rester prudents et circonspects avec l'HR tant qu'aucune démonstration complète ne vient la confirmer ou l'infirmer. Et bien évidemment ça ne vaut pas que pour l'HR, mais pour tout ce qui porte le nom de conjecture.
est une approximation de pi qui a plus de 42 milliards de décimales exactes. Si l'on avait du rendre un jugement seulement sur la base de quelques millions de décimales, on se serait salement trompés... il convient donc de rester prudents et circonspects avec l'HR tant qu'aucune démonstration complète ne vient la confirmer ou l'infirmer. Et bien évidemment ça ne vaut pas que pour l'HR, mais pour tout ce qui porte le nom de conjecture.
Modifié en dernier par L.A. le 20 Jan 2017, 19:44, modifié 1 fois.
Re: Le point sur l'hypothèse de Riemann
L.A. a écrit:D'après le livre de JP Delahaye "Le fascinant nombre pi", le nombre défini par
est une approximation de pi qui a plus de 42 milliards de décimales exactes.










Il dit comment on prouve que c'est pas pi? Parce que j'imagine qu'à ce stade c'est pas un ordi qui nous l'a dit.
Re: Le point sur l'hypothèse de Riemann
Non, il dit juste que ce résultat a été prouvé en 1992 par J. et P. Borwein, mais je n'ai pas trouvé d'autre référence à ce sujet... Ce qui serait aussi intéressant, c'est de savoir d'où sort cette série ou l'idée de la comparer à pi.
Re: Le point sur l'hypothèse de Riemann
Le théorème du fainéant affirme que quand il s'agit d'une série bizarre Ramanujan en est l'auteur 
Il y a ça sur les intégrales de Borwein :
https://sciencetonnante.wordpress.com/2012/07/16/les-integrales-de-borwein/
ça ressemble vachement, ils ont dû modifier deux trois trucs, ils disent aussi des mots sur Wikipédia!
Il y a ça sur les intégrales de Borwein :
https://sciencetonnante.wordpress.com/2012/07/16/les-integrales-de-borwein/
ça ressemble vachement, ils ont dû modifier deux trois trucs, ils disent aussi des mots sur Wikipédia!
Re: Le point sur l'hypothèse de Riemann
Si on part deL.A. a écrit:Ce qui serait aussi intéressant, c'est de savoir d'où sort cette série ou l'idée de la comparer à pi.
Et l'erreur commise, (entre la somme de Riemann et l'intégrale), elle vaut dans les combien ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Le point sur l'hypothèse de Riemann
Haha tu casses le mythe, je pensais qu'elle avait été trouvée par hasard et qu'il y avait beaucoup de mystère derrière tout ça ^^
Si ça marche comme ça dans une semaine je sors un bouquin "le fascinant nombre e"
Si ça marche comme ça dans une semaine je sors un bouquin "le fascinant nombre e"
Re: Le point sur l'hypothèse de Riemann
Euh... 42 milliards de décimales exactes, quand même pas ?
je vois bien l'erreur commise en O(dt²), donc une dizaine ou une quinzaine de décimales exactes, je veux bien, un peu plus si il y a un meilleur exposant etc, mais ça reste très très loin du milliard.
je vois bien l'erreur commise en O(dt²), donc une dizaine ou une quinzaine de décimales exactes, je veux bien, un peu plus si il y a un meilleur exposant etc, mais ça reste très très loin du milliard.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
