Bases arithmétique trigonométrique
13 messages
- Page 1 sur 1
Bases arithmétique trigonométrique
Bonjour .
Voici une construction géométrique qui donne le carré d'une longueur , ici OB = OA * OA . On effectue une élévation au carré en doublant l'angle formé par le cosinus alpha . La forme exacte :
Cos alpha = 1 / OA
OA*OA = ( 1 / ( ( 1 + cos ( 2* alpha)) / 2 )
Déterminer une racine consiste à partir de OB arriver en OA mais je n'ais pas encore trouvé la forme algébrique .
Voici une construction géométrique qui donne le carré d'une longueur , ici OB = OA * OA . On effectue une élévation au carré en doublant l'angle formé par le cosinus alpha . La forme exacte :
Cos alpha = 1 / OA
OA*OA = ( 1 / ( ( 1 + cos ( 2* alpha)) / 2 )
Déterminer une racine consiste à partir de OB arriver en OA mais je n'ais pas encore trouvé la forme algébrique .
Re: Bases arithmétique trigonométrique
Modifié en dernier par AlainRatomahenina le 22 Sep 2017, 08:07, modifié 1 fois.
Re: Bases arithmétique trigonométrique
Ce qui est amusant , c'est que l'on pourrait fabriquer une mécanique , suivant le principe géométrique , avec OA gradué de 0 à 10 et OB de 0 à 100 .
Vous imaginez si on avait pu avoir ça au moyen âge ?
Mais le but de cette base arithmétique est de pouvoir réaliser toutes les opérations de base . Voyez vous comment faire ?
Vous imaginez si on avait pu avoir ça au moyen âge ?
Mais le but de cette base arithmétique est de pouvoir réaliser toutes les opérations de base . Voyez vous comment faire ?
Re: Bases arithmétique trigonométrique
Je dois vous dire que je n'aîs pas réussi à trouver la forme algébrique de la racine carrée , autant géométriquement il est simple de tracer la longueur racine d'une autre longueur . Mais il y a longtemps , je savais le faire ; il faut maintenant retrouver cette forme algébrique .
Re: Bases arithmétique trigonométrique
Voici donc la multiplication trigonométrique . Il suffit en fait d'appliquer géométriquement la formule du produit de deux cosinus : cos a * cos b = ( cos ( a - b ) + cos ( a + b )) / 2 et on peut effectuer une multiplication en additionnant et en soustrayant de simples angles .
http://hpics.li/58b7aed
http://hpics.li/58b7aed
Re: Bases arithmétique trigonométrique
Ce qu'il faut savoir c'est que l'inverse d'un nombre correspond au cosinus d'un angle . En additionnant ou en soustrayant ces angles on obtient un nouveau cosinus . L'inverse de ce cosinus donnera un nombre correspondant au resultat de l'opération arithmétique .
On peut facilement concevoir une machine mécanique pour effectuer les opérations de base et les racines carrées . Dire qu' on aurait pu avoir ça au moyen âge ....
On peut facilement concevoir une machine mécanique pour effectuer les opérations de base et les racines carrées . Dire qu' on aurait pu avoir ça au moyen âge ....
Re: Bases arithmétique trigonométrique
Bonjour...
Assez flou ce que tu veux faire. Cherches-tu à construire la racine carrée d'un nombre avec une méthode géométrique? ...
Assez flou ce que tu veux faire. Cherches-tu à construire la racine carrée d'un nombre avec une méthode géométrique? ...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Bases arithmétique trigonométrique
Il s'agit en fait d'une arithmétique complète , réalisable grâce au tracé de longueurs . Oui , je veux calculer géométriquement une racine carrée par exemple , ce qui est possible grâce à mon système . Je regrette que cela te semble flou mais je pensais avoir clairement exposé le sujet : Il faut mieux regarder pour bien comprendre .
Re: Bases arithmétique trigonométrique
Salut,
Ca peut effectivement être amusant de chercher d'autres méthodes (forcément plus compliquées), mais on sait depuis au moins les grecs anciens (voire avant) comment réaliser des multiplication/division géométriquement.
Et évidement, LE outil qui va bien, c'est simplement Thales où, dans la configuration "standard" (deux sécantes en O plus deux parallèles, la première coupant les sécantes en A et A' et la deuxième en B et B'), les distances des 4 points d'intersection à O sont liés par la formule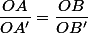 (=rapport de projection).
(=rapport de projection).
Donc, si par exemple on veut calculer le carré d'une longueur L donnée, on construit deux sécantes (quelconques), sur une sécante on construit A et B tels que OA=1 et OB=L et sur l'autre A' tel que OA'=L et il suffit de mener la parallèle à (AA') passant par B pour obtenir B' tel que OB'=L².
Idem pour tout autre produit LxL' ou division L/L' (dans les deux cas, il faut évidement connaitre un segment de longueur unité vu que la valeur numérique du résultat dépend de l'unité choisie, par contre pour calculer un truc du style L x L' / L'' dont le résultat est indépendant de l'unité choisie, il n'est pas utile de connaitre la longueur du segment unité)
Par contre, pour la construction des racines carrées, c'est légèrement moins trivial (mais connu depuis au moins Euclide vers 300 av JC) : tape sur le net "construction géométrique d'une racine carrée" et tu trouvera des tas de méthodes (dont celle proposée par Euclide).
Remarque : De même, pour calculer racine(L), il faut forcément connaitre la longueur de l'unité vu que la valeur numérique du résultat en dépend, mais ce n'est pas utile pour calculer racine(LxL')
Ca peut effectivement être amusant de chercher d'autres méthodes (forcément plus compliquées), mais on sait depuis au moins les grecs anciens (voire avant) comment réaliser des multiplication/division géométriquement.
Et évidement, LE outil qui va bien, c'est simplement Thales où, dans la configuration "standard" (deux sécantes en O plus deux parallèles, la première coupant les sécantes en A et A' et la deuxième en B et B'), les distances des 4 points d'intersection à O sont liés par la formule
Donc, si par exemple on veut calculer le carré d'une longueur L donnée, on construit deux sécantes (quelconques), sur une sécante on construit A et B tels que OA=1 et OB=L et sur l'autre A' tel que OA'=L et il suffit de mener la parallèle à (AA') passant par B pour obtenir B' tel que OB'=L².
Idem pour tout autre produit LxL' ou division L/L' (dans les deux cas, il faut évidement connaitre un segment de longueur unité vu que la valeur numérique du résultat dépend de l'unité choisie, par contre pour calculer un truc du style L x L' / L'' dont le résultat est indépendant de l'unité choisie, il n'est pas utile de connaitre la longueur du segment unité)
Par contre, pour la construction des racines carrées, c'est légèrement moins trivial (mais connu depuis au moins Euclide vers 300 av JC) : tape sur le net "construction géométrique d'une racine carrée" et tu trouvera des tas de méthodes (dont celle proposée par Euclide).
Remarque : De même, pour calculer racine(L), il faut forcément connaitre la longueur de l'unité vu que la valeur numérique du résultat en dépend, mais ce n'est pas utile pour calculer racine(LxL')
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Bases arithmétique trigonométrique
Salut Ben,
Il existe des nombres qui ne sont pas constructibles (à la règle et au compas) une fois j'ai fait un TD sur ça...
Donc il faut bien conclure qu'on ne peut pas construire tous les nombres (je ne comprends pas le sens de 'arithmétique complète' vu qu'on tombe sur des irrationnels assez rapidement??).
Il existe des nombres qui ne sont pas constructibles (à la règle et au compas) une fois j'ai fait un TD sur ça...
Donc il faut bien conclure qu'on ne peut pas construire tous les nombres (je ne comprends pas le sens de 'arithmétique complète' vu qu'on tombe sur des irrationnels assez rapidement??).
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Bases arithmétique trigonométrique
Je le répète , ce système géométrique permet de concevoir une machine à calculer , mécanique articulée en deux dimensions , ce qui pourrait être très intéressant . Ceci ne vous avait pas semblé évident ? Cette mécanique est irréalisable par les méthodes que tu m'a décrit .
Ça ne vous semble pas étonnant d'effectuer une multiplication ou déterminer une racine carrée simplement en additionnant de simples angles ?
Ça ne vous semble pas étonnant d'effectuer une multiplication ou déterminer une racine carrée simplement en additionnant de simples angles ?
Re: Bases arithmétique trigonométrique
AlainRatomahenina a écrit:Je le répète , ce système géométrique permet de concevoir une machine à calculer , mécanique articulée en deux dimensions , ce qui pourrait être très intéressant . Ceci ne vous avait pas semblé évident ? Cette mécanique est irréalisable par les méthodes que tu m'a décrit .
Ça ne vous semble pas étonnant d'effectuer une multiplication ou déterminer une racine carrée simplement en additionnant de simples angles ?
Tu dis absolument n'importe quoi ou presque. Explique.
C'est quoi une "mécanique articulée en deux dimensions" ?
Pourquoi cette 'mécanique' est "irréalisable" avec ce qu'on te décrit?
En quoi faire intervenir des formules de trigonométrie et des angles est-il plus 'simple' que d'extraire une racine directement par la géométrie euclidienne? Bon je ne dis pas que c'est pas intéressant, mais un peu d'humilité ne te ferait pas de mal je crois.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Bases arithmétique trigonométrique
Là réalisation du calcul de racines carrées est irréalisable par les procédés qui existe car ce sont des constructions géométrique théoriques . Chaque valeur est traitée cas par cas .
Vous voyez bien que l'on peut réaliser une machine avec des parralellogrammes articulés pour additionner les angles formés par l'orientation des règle des opérandes .
Certains disent , comme l'APMEP , que c'est Descartes qui a établi le premier ce genre de constructions et non pas les grecs , même si on utilise le théorème de Thalès .
Vous voyez bien que l'on peut réaliser une machine avec des parralellogrammes articulés pour additionner les angles formés par l'orientation des règle des opérandes .
Certains disent , comme l'APMEP , que c'est Descartes qui a établi le premier ce genre de constructions et non pas les grecs , même si on utilise le théorème de Thalès .
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
