Une fraction
Réponses à toutes vos questions du CP à la 3ème
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 27 Juil 2017, 07:06
par Dacu » 27 Juil 2017, 07:06
Bonjour à tous,
Soit
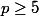
un nombre premier et

sorte que

.Montrer que les nombres

et

donner même reste de la division avec

.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 27 Juil 2017, 07:39
par pascal16 » 27 Juil 2017, 07:39
Je me vois mal faire une récurrence niveau collège
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 28 Juil 2017, 05:31
par Dacu » 28 Juil 2017, 05:31
pascal16 a écrit:Je me vois mal faire une récurrence niveau collège
Bonjour,
Ce problème a été proposé dans le concours de mathématiques pour la classe VII de la Roumanie, assimilais, dis-je, pour le collège en France....A quel niveau pourrait être le problème?Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Juil 2017, 14:56
par aymanemaysae » 28 Juil 2017, 14:56
Bonjour ;
Soient

l'ensemble des nombres entiers naturels premiers , et

, on a donc :
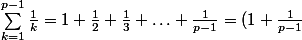+ (\frac{1}{2} + \frac{1}{p-2}) + \ldots + (\frac{1}{\frac{p-1}{2}} + \frac{1}{p-\frac{p-1}{2}}))
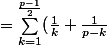 = \sum_{k=1}^{\frac{p-1}{2}} \frac{p}{k(p-k)} = p \sum_{k=1}^{\frac{p-1}{2}} \frac{1}{k(p-k)} .)
Posons
})
, donc :

,
donc :
 p - 1}{p - 1} = \frac{a}{b})
avec
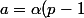 p - 1)
et

, donc

donc

,
donc a et b sont premiers entre-eux , et

et

.
-
Arbre
 par Arbre » 28 Juil 2017, 15:04
par Arbre » 28 Juil 2017, 15:04
Bonjour,
J'ai 1+1/2+1/3+1/4+1/5=137/60;
137 mod 7 = 60 mod 7 =4 diffèrent de 6=-1 mod 7.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Juil 2017, 15:16
par aymanemaysae » 28 Juil 2017, 15:16
Bonjour ;
tu as raison , mais je ne vois pas d'où vient l'erreur .
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Juil 2017, 15:19
par aymanemaysae » 28 Juil 2017, 15:19
Bonjour ;
je m'excuse : l'erreur vient du

que j'ai mise au numérateur et que j'ai confondue avec un nombre entier naturel .
-
Arbre
 par Arbre » 28 Juil 2017, 15:23
par Arbre » 28 Juil 2017, 15:23
Bonjour,
On calcule :
=\frac{1}{(p-1)!}(\sum\limits_{k=1}^{p-2} \frac{(p-1)!}{k}))
On a
! \mod p=1)
!}{k} \mod p= 1+\sum \limits_{k=1}^{p-1} \frac{1}{k} \mod p=1)
Donc il existe

premier avec p tel que

d'où le résultat.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Juil 2017, 15:34
par aymanemaysae » 28 Juil 2017, 15:34
Bonjour ;
Bravo , c'est vraiment élégant et ingénieux , surtout la première ligne de la démonstration .
-
Arbre
 par Arbre » 28 Juil 2017, 15:35
par Arbre » 28 Juil 2017, 15:35
Merci.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Juil 2017, 20:07
par aymanemaysae » 28 Juil 2017, 20:07
Bonsoir ;

soient

l'ensemble des nombres entiers naturels premiers , et

, on a donc :
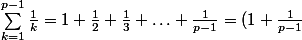+ (\frac{1}{2} + \frac{1}{p-2}) + \ldots + (\frac{1}{\frac{p-1}{2}} + \frac{1}{p-\frac{p-1}{2}}))
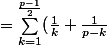 = \sum_{k=1}^{\frac{p-1}{2}} \frac{p}{k(p-k)} = p \sum_{k=1}^{\frac{p-1}{2}} \frac{1}{k(p-k)} .)
Posons
})
, avec
\in \mathbb N^{*2})
donc :

,
donc :
 p - v}{v(p - 1)} })
avec

et

on a :
-\alpha)p - \beta}{(\alpha (p-1) + \beta)p - \beta})
: CQFD
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités