Salut;
je me bloque sur cet exercice :
Soit f une fonction définie de [0;1] dans [0;1] et continue sur [0;1]
établir que : ( ∃c ∈ [0;1] ) f(c)+f(1-c)=2c
j'ai essayé d'utiliser le theoreme de valeur intermédiaire en posant :
g(c)=f(c)+f(1-c)-2c=0
et g est continue sur [0;1]
puis j'ai trouvé: g(1)=f(1)+f(0)-2
et g(0)=f(0)+f(1)
mais j'ai aucune idée comment je peux justifié que g(1)*g(0)< 0
un petit indice ?
merci d'avance!
T.V.I
3 messages
- Page 1 sur 1
Re: T.V.I
Bonjour,
Et ainsi ... ?
f(x) = f(1-x) pour x = 1/2
En posant f(1/2) = c, il vient, pour x = 1/2 : f(c) + f(1-c) = c + c = 2c

Et ainsi ... ?
f(x) = f(1-x) pour x = 1/2
En posant f(1/2) = c, il vient, pour x = 1/2 : f(c) + f(1-c) = c + c = 2c
Re: T.V.I
Black Jack s'est trompé(*), revenons à ta démarche qui est la bonne : considérer la fonction +f(1-x)-2x) .
.
Peux-tu comparer) à 0 ?
à 0 ?
Peux-tu comparer) à 0 ?
à 0 ?
Et conclure ? (Petit coup de pouce : rien n'interdit à d'être égal à 0 ou à 1 !)
d'être égal à 0 ou à 1 !)
(*) Un petit exemple : soit qui satisfait bien les hypothèses de l'énoncé. Alors
qui satisfait bien les hypothèses de l'énoncé. Alors =1/4) et
et +f(1-1/4)=5/8) qui est bien sûr différent de
qui est bien sûr différent de 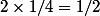 .
.
Peux-tu comparer
Peux-tu comparer
Et conclure ? (Petit coup de pouce : rien n'interdit à
(*) Un petit exemple : soit
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
