Le théoréme de Pythagore

[la_plus_nul_en_maths]

J'aimerais en savoir plus car on est en train de commencer et je comprend pas trop et on commence aussi les racines que je comprend pas trop aussi qq peut m'expliquer en principe comment ca fonctionne.

[mathador]

Salut
Théorème de Pythagore : Si on a un triangle rectangle de côtés de longueurs a,b et c (c étant l'hypothénuse), alors a² + b² = c². La réciproque est vraie : si a² + b² = c², alors le triangle est rectangle et c est l'hypothénuse. Y'a rien à comprendre, c'est une propriété, comme Thalès si tu l'as déjà vu :id:

Les racines carrées. On te donne un nombre n > 0. Pour passer de n à n², pas de problème, tu élèves au carré. Mais pour passer de n² à n ????? Et bien c'est cela, la racine carré : c'est l'outil qui nous permet, pour un nombre positif A, de trouver le nombre (lui aussi positif) dont le carré vaut A.
Exemples : racine de 25 = 5. En effet, 5² = 25.
racine de 49 = 7. Eh oui, 7² = 49.
racine de -81? Ceux qui répondent 9 ou -9 ont perdu : j'ai dit que le nombre à mettre sous la racine doit être POSITIF !!!!
Racine de 3 ? ah, là, on a plus de mal à répondre ! contrairement à 49 par exemple, 3 n'est pas un carré parfait. Sa racine carrée vaut environ 1,73205081. Tu peux vérifier que ce nombre au carré donne presque 3 ... mais pas tout à fait : la valeur exacte, c'est simplement racine de 3 (je n'en dis pas plus pour ne pas sortir du programme ... l'irrationalité sera vue plus tard !).

Noter enfin ces quelques propriétés immédiates et très très utiles (tu le verras en faisant des exos) :
pour a>0 ,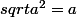
et pour tout a , (a si a>0) ou (-a si a<0) ou (0 si a=0)
(je sais pas si ça se voit au collège, mais pour faire plus simple on peut dire que pour tout a , )

dernier nota pour les puristes : quand je dis "pour tout a", je parle naturellement de nombres réels, les seuls connus au collège.

Voilà, n'hésite pas à demander plus d'explications !

[la_plus_nul_en_maths]

quand on dit par exemple ABC est un triangle rectangle en A et que AB = 6cm et que AC = 5cm calculer BC en fait il faut calculer l'hypothenuse fin c'est a dire on écrit l'hypothénuse qui est obligatoirement BC donc ça fera
BC au carré = AC au carré + AB au carré non ?

en gros on est écrit toujours l'hypothénuse en premier
BC au carré =.....non ?

[moroccan]

Ecrire BC² = AC² + AB²
c'est juste, si comme tu dis au début ABC est rectange en A

Mais pour l'ordre, ça n'a pas d'importance: écrire BC² = AC² + AB² ou
AC² + AB² = BC², c'est absolument la même chose..

[la_plus_nul_en_maths]

ok ! merci beaucoup ! à tous