Nombres rationnels et puissances .

[MATH&ME]

A) est le point de croisement de la bissectrice de .
Calculer l'aire de ADC si aire ABC = 20 cm²


B) On met :

S1 = aire ABH
S2 = aire ACH
l'aire de ABC = 33 cm²
Calculer si :



C) On a :

Donner le resultat ainsi que la méthode suivie .
D) Trouver x :

E)
Trouver x.

F) Calculer :
[a^5*b^6*(c^(-3))]/[a^7*b^8*(c^(-5))]
J'ai mis : (abc)^(-2)
Apres verifier si :

[Kikoo <3 Bieber]

Salut !

C'est sûr que le niveau en maths des élèves de collège dans certains pays arabes est plus élevé que le nôtre... :hum:

Pour la première question, je ne vois pas d'autres façons qu'utiliser la loi des sinus et le théorème d'Al Kashi. Il doit y avoir d'autres moyens, car ces outils sont un peu trop sophistiqués.

Pour la deuxième question, il manque des données, car on peut déjà formellement déterminer S1 grâce au rapport fourni. Ce serait trop simple...

Pour la troisième question, on réécrit ce nombre . C'est un piège de "noobzor" cet exo, car on remarque que lorsque k vaut 27, cela termine le calcul.

Pour le quatrième exo, euh... On peut utiliser la calto, nan ?

Pour le cinquième exo, tu t'es trompé(e). Je te laisse me montrer ce que t'as fait.
Je n'ai pas compris ton "vérifier que ab=3c", sachant que l'on a pas d'égalité.

[MATH&ME]

Salut .

Enfait je trouve ces exercices plutot difficiles à résoudre avec des outil collége .
Alors pour A quelle est la méthode à utiliser meme si je n'ai pas encore étudié le sinus et l théorém d'al kashy .??
B) j'ai oublié de noter l'aire de ABC = 33 cm²
C) je ne sais pas la signification du symbole ainsi que toute l'expression ; je peut faire un calcul normale mais il faut une façon rapide pour terminer le calcul .
D) we jepeux utiliser la calculatrie mais comment ??? si ca peut se faire sans calculatrice ca serai mieu .
E) je vais eessayer de poster la bonne reponse .
Pour ab=3c , a,b,c sont des nombres non nuls , on me demande de justifier ab=3c ; je crois qu'elle à un rapport avec le calcul au dessus .

[Kikoo <3 Bieber]

Pour la A)... j'y réfléchis.

Pour la B), tu n'as qu'à appliquer un produit en croix alors.
Pour la C), je t'ai déjà donné la réponse Que se passe-t-il au 27ème facteur ?
Pour la D), c'est vrai que tu n'as pas encore vu les fonctions réciproques. Mais pensons-y : Si , alors que peux-tu dire de x ? N'existe-t-il que des racines carrées ?
Je sais, je suis pas très clair.
Pour la E), je ne vois toujours pas en quoi on peut justifier que ab=3c.


Ah oui, pour la B, le symbole que je t'ai donné se lit "le produit des 1-(k/27) quand k va de 1 à 50"

[Lostounet]

Yo,

Pour le A)
Il me semble qu'il y a un problème avec les valeurs numériques..

Mais en gros, une méthode:

* On calcule l'angle en utilisant la formule suivante: (ABC) désigne l'aire du triangle ABC:

2(ABC) = AB*AC*sin(BAC)

* En utilisant la formule d'Al-Kashi, on trouve la longueur BC

* AD est une bissectrice dont la longueur est donnée par:



* On applique de nouveau la 1ere formule et on trouve l'aire demandée...


Une autre méthode plus astucieuse:
On sait que ABD) et ADC ont même hauteur, on déduit donc que le rapport d'aires (ABD)/(ADC) = CD/BD

Nous pouvons démontrer que ce rapport d'aires est égal à 15/8 (Car CD/BD = AC/AB)

De plus, la somme de ces deux aires est de 20.

Soit y = (ABD) et x = (ADC)

x et y sont donc solution du système:

x + y = 20
x/y = 15/8

[Lostounet]

Pour la deuxième question, il manque des données, car on peut déjà formellement déterminer S1 grâce au rapport fourni. Ce serait trop simple...

Hum?


S1 + S2 = 33
S1/S2 = 4/7

[Kikoo <3 Bieber]

Hum?


S1 + S2 = 33
S1/S2 = 4/7

Mon Dieu O_O J'avais pas vu que l'aire totale était donnée...
C'est décidé, je vais dormir.

[MATH&ME]

Alors pour A ca reste flou .
pour B ) :
S1 = aire ABH
S2 = aire ACH
l'aire de ABC = 33 cm²
S1/S2= 4/7 ou S1*7 = S2*4
S1=4/7 * S2
S2=S1/(4/7)
S2*4 = (4/7 * S2)*7
S1*7 = (S1/(4/7))*4
Est ce la bonne méthode pour resoudre l'equation ????

[Lostounet]

Alors pour A ca reste flou .

Voici une explication détaillée car l'exo peut paraître un peu difficile.

Tu as deux triangles ADC et ADB. Tu les vois bien?

Ce deux triangles ont la même hauteur... (Celle issue de A)
Il suffit de tracer une perpendiculaire issue de A sur (BD), pour voir que cette hauteur est la même pour les deux triangles (une hauteur dans un triangle n'est pas toujours à l'intérieur du triangle).

Alors, je disais que ces deux triangles ont même hauteur de longueur h.

L'aire de (ADC) est et l'aire de (ADB) est . Tu es d'accord?

Je vais désigner par x l'aire de (ADC) et y l'aire de (ADB)...

Je vais calculer :





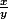
Diviser par une fraction, c'est multiplier par son inverse:




On simplifie en haut et en bas par 2 et par h, on trouve finalement:



Tu es d'accord? Ok.
Pourquoi j'ai calculé x/y ? Voilà pourquoi:

Ensuite, on va utiliser la propriété suivante de la bissectrice: http://en.wikipedia.org/wiki/Angle_bisector_theorem
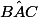
Comme (AD) est la bissectrice de l'angle , on peut appliquer ce théorème qui dit que:

si [AD] est bissectrice, CD/BD = AC/AB


On sait que AC/AB = ... (Calcule !)

Donc CD/BD = ...

Or CD/BD c'est en fait x/y, donc x/y fait aussi ....



Maintenant, tu sais que l'aire totale du triangle fait 20 cm^2, donc x + y = 20
Tu viens de calculer x/y = ...

Tu obtiens un système de deux équations à deux inconnues... Tu peux trouver la valeur de x.

[Lostounet]

pour B ) :
S1 = aire ABH
S2 = aire ACH
l'aire de ABC = 33 cm²
S1/S2= 4/7 ou S1*7 = S2*4
S1=4/7 * S2
S2=S1/(4/7)
S2*4 = (4/7 * S2)*7
S1*7 = (S1/(4/7))*4
Est ce la bonne méthode pour resoudre l'equation ????

Je ne comprends pas ce que tu as fait... C'est juste mais ça ne nous avance pas.

S1 + S2 = 33
S1/S2 = 4/7

Nous allons appliquer la méthode par substitution:

D'après la 1ere équation: S1 = 33 - S2

D'après la 2e équation:

(33 - S2)/S2 = 4/7
Donc:

7(33 - S2) = 4 * S2
C'est une équation du premier degré à une seule inconnue... Facile à résoudre

Tes exercices sont toujours intéressants

[MATH&ME]

J'ai enfait avancé au niveau des cours , je vais essayer aprés de résoudre A
Maintenant comment résoudre
E)
Trouver x.
Alors pour celle ci je vois que c'est :
x^5 = 759375.10^(-5)
= 759375.[(10^(-1))^5]
Mais comment connaitre x .??

[Lostounet]

J'ai enfait avancé au niveau des cours , je vais essayer aprés de résoudre A
Maintenant comment résoudre
E)
Trouver x.
Alors pour celle ci je vois que c'est :
x^5 = 759375.10^(-5)
= 759375.[(10^(-1))^5]
Mais comment connaitre x .??

C'est un peu délicat.

Tu sais résoudre x^5 = 32 ?

Une équation de la forme a pour solution:

Désigne le nombre qui, multiplié par lui-même 5 fois, donne a.

x^5 = 32

On remarque que

Donc , donc x = 2... On peut écrire


Pour ton équation , on peut remarquer:

759375 = 15^5

L'équation devient:



Donc x = ...

[MATH&ME]

C'est un peu délicat.

Tu sais résoudre x^5 = 32 ?

Une équation de la forme a pour solution:

Désigne le nombre qui, multiplié par lui-même 5 fois, donne a.

x^5 = 32

On remarque que

Donc , donc x = 2... On peut écrire


Pour ton équation , on peut remarquer:

759375 = 15^5

L'équation devient:



Donc x = ...

Merci lostounet .

J'apprécie vraiment tes éxplications

[Lostounet]

De rien :)

Tu peux poser tes questions ou d'autres problèmes. J'espère être en train de t'aider à progresser.

[MATH&ME]

De rien

Tu peux poser tes questions ou d'autres problèmes. J'espère être en train de t'aider à progresser.

Enfait tu m'aide vraiment à passer certains obstacles .
Je te souhaite un bon ramadan au passage .

[Lostounet]

:)

Bon Ramadan à toi aussi.

[Shew]

Je me demande si n'est pas un angle droit parce que la loi des sinus et des cosinus au college cela me semble un tiré par les cheveux .

[Lostounet]

On peut utiliser des résultats issus de la loi des sinus/ Al-Kashi concernant la bissectrice et le rapport d'aires des deux triangles... (Rapport des deux côtés qui engendrent la bissectrice).

Ou sinon passer par des méthodes plus calculatoires, notamment avec le résultat du théorème de Stewart sur la longueur de la bissectrice en fonction des côtés/ Al-kashi pour le calcul d'aires, angles, des côtés...). J'ai l'impression que tout passe par Al-kashi finalement !

Mais il faut avoir déjà vu tt ça quelque part sinon c'est dur.

[Shew]

!

Mais il faut avoir déjà vu tt ça quelque part sinon c'est dur.

Ce qui ne semble pas être le cas de MATH&ME ->

Alors pour A quelle est la méthode à utiliser meme si je n'ai pas encore étudié le sinus et l théorém d'al kashy .??

d'ou ma question . Je pense que la figure n'est pas complete , de plus , nous avons les valeurs de deux côtés données ce qui me laisse penser a pythagore .

[Lostounet]

Bah un bon cours de géométrie sur les bissectrices suffit :)

Si le triangle est rectangle, ça devient plus simple, c'est quand même un bon entraînement.