Bonjour je ne comprends pas du tout ce chapitre ,
Les mèthodes par substitution , graphique , combinaison .
Je ne comprends mais vraiment rien du tout : /
Les systémes d'équations du premier degré à une inconnue
9 messages
- Page 1 sur 1
bonsoir,
exemple :
x+y=5 (1)
{
2x+3y=8 (2)
substitution :
d'après (1) x=5-y
on remplace dans (2)
2(5-y)+3y=8
10-2y+3y=8
10+y=8
y=-10+8
y=-2
remplaçons dans x=5-y=5-(-2)=5+2=7
le couple solution {7;-2}
par combinaison :
x+y=5 (1)
{
2x+3y=8 (2)
on multiplie (1) par -2, on a le système équivalent
-2x-2y=-10
{
2x+3y=8 (2)
additionnons (1)+(2)=-2x-2y+2x+3y=-10+8
-2y+3y=-2
y=-2
on remplace dans (1):
x+(-2)=5
x-2=5
x=5+2
x=7
graphiquement
x+y=5
y=5-x---> trace la droite correspondant à cette fonction affine
2x+3y=8
3y=8-2x
y=-2/3x+8/3---> trace la droite correspondant à cette fonction affine
les coordonnées du point de concours de ces 2 droites est le couple solution du systèmeà 2 inconnues
exemple :
x+y=5 (1)
{
2x+3y=8 (2)
substitution :
d'après (1) x=5-y
on remplace dans (2)
2(5-y)+3y=8
10-2y+3y=8
10+y=8
y=-10+8
y=-2
remplaçons dans x=5-y=5-(-2)=5+2=7
le couple solution {7;-2}
par combinaison :
x+y=5 (1)
{
2x+3y=8 (2)
on multiplie (1) par -2, on a le système équivalent
-2x-2y=-10
{
2x+3y=8 (2)
additionnons (1)+(2)=-2x-2y+2x+3y=-10+8
-2y+3y=-2
y=-2
on remplace dans (1):
x+(-2)=5
x-2=5
x=5+2
x=7
graphiquement
x+y=5
y=5-x---> trace la droite correspondant à cette fonction affine
2x+3y=8
3y=8-2x
y=-2/3x+8/3---> trace la droite correspondant à cette fonction affine
les coordonnées du point de concours de ces 2 droites est le couple solution du systèmeà 2 inconnues
bonjour,
il y a trois méthodes de résolutions des systèmes:
(1) par combinaison linéaire d'égalités. On couple cette méthode avec le pivot de Gauss
(2) par substitution
(3) avec un calcul de déterminants
méthode 1:méthode du pivot
soit le système à 3 inconnues
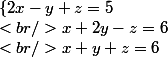
On prend l'inconnue x comme pivot dans la troisième égalité. On choisit la 3ème égalité car le coefficient de x est 1 (1x=x)
on soustrait une fois la dernière égalité de la seconde
et deux fois la dernière égalité de la première. il vient:
=5-12 \\<br />x+2y-z-(x+y+z)=6-6 \\<br />x+y+z=6)
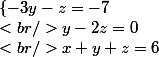
On prend l'inconnue y comme pivot dans la deuxième égalité. On choisit la 2ème égalité car le coefficient de y est 1 (1y=y)
on additionne trois fois la deuxième égalité à la première
=-7+3 \times 0 \\<br />y-2z=0 \\<br />x+y+z=6)
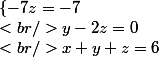
la 1ère égalité donne z=1, la seconde y=2,la troisième x=3.
méthode 2:méthode de substitution
substituer=remplacer.
l'aspartam des sucrettes est un substitut du sucre.
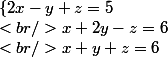
on calcule x dans la troisième égalité, en fonction de y et z
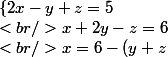)
on remplace x (on substitue x) par sa formule dans les deux autres égalités
\right) -y+z=5 \\<br />6-(y+z)+2y-z=6 \\<br />x=6-(y+z))
on réduit dans les deux premières égalités
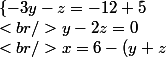)
les deux premières égalités donnent un système de deux équations à deux inconnues. on calcule y avec la seconde égalité
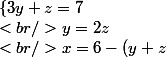)
on remplace y dans la 1ère égalité par son expression en fonction de z.
+z=7 \\<br />y=2z \\<br />x=6-(y+z))
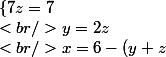)
la 1ère égalité donne z=1, la seconde y=2, la troisième x=3.
méthode 3:méthode des déterminants
la méthode des déterminants est utilisée quand les coefficients des inconnues
ne sont plus des fractions mais des racines carrées ou des lettres a,b,c..
je ne l'explique pas. c'est au programme du lycée.
il y a trois méthodes de résolutions des systèmes:
(1) par combinaison linéaire d'égalités. On couple cette méthode avec le pivot de Gauss
(2) par substitution
(3) avec un calcul de déterminants
méthode 1:méthode du pivot
soit le système à 3 inconnues
On prend l'inconnue x comme pivot dans la troisième égalité. On choisit la 3ème égalité car le coefficient de x est 1 (1x=x)
on soustrait une fois la dernière égalité de la seconde
et deux fois la dernière égalité de la première. il vient:
On prend l'inconnue y comme pivot dans la deuxième égalité. On choisit la 2ème égalité car le coefficient de y est 1 (1y=y)
on additionne trois fois la deuxième égalité à la première
la 1ère égalité donne z=1, la seconde y=2,la troisième x=3.
méthode 2:méthode de substitution
substituer=remplacer.
l'aspartam des sucrettes est un substitut du sucre.
on calcule x dans la troisième égalité, en fonction de y et z
on remplace x (on substitue x) par sa formule dans les deux autres égalités
on réduit dans les deux premières égalités
les deux premières égalités donnent un système de deux équations à deux inconnues. on calcule y avec la seconde égalité
on remplace y dans la 1ère égalité par son expression en fonction de z.
la 1ère égalité donne z=1, la seconde y=2, la troisième x=3.
méthode 3:méthode des déterminants
la méthode des déterminants est utilisée quand les coefficients des inconnues
ne sont plus des fractions mais des racines carrées ou des lettres a,b,c..
je ne l'explique pas. c'est au programme du lycée.
[quote]
Posté par yvelines78
les systèmes à 3 inconnues ne sont pas abordées au collège
Euh ptet mais quand on sait faire avec 2, il faut pas se creuser la cervelle bien longtemps pour comprendre comment faire avec 50. Evidemment avec 50 c'est plus délicat mais pas plus difficile !!!
Hier 19h52[\QUOTE]
mais quand on démarre une nouvelle notion et qu'on a du mal à l'assimiler pourquoi compliquer la tâche!!!!!
Posté par yvelines78
les systèmes à 3 inconnues ne sont pas abordées au collège
Euh ptet mais quand on sait faire avec 2, il faut pas se creuser la cervelle bien longtemps pour comprendre comment faire avec 50. Evidemment avec 50 c'est plus délicat mais pas plus difficile !!!
Hier 19h52[\QUOTE]
mais quand on démarre une nouvelle notion et qu'on a du mal à l'assimiler pourquoi compliquer la tâche!!!!!
Sve@r a écrit:Euh ptet mais quand on sait faire avec 2, il faut pas se creuser la cervelle bien longtemps pour comprendre comment faire avec 50. Evidemment avec 50 c'est plus délicat mais pas plus difficile !!!
mais quand on démarre une nouvelle notion et qu'on a du mal à l'assimiler pourquoi compliquer la tâche!!!!!
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
