On peut aussi faire un raisonnement diffèrent.
Pour déterminer l'étage, on considère que lors de la construction, on économise une brique tous les deux étages (et décalant leur position pour que le mur tienne et soit à peu près de la largeur souhaitée). Donc, si on n'avait pas économisé les briques, la
n-ième brique du mur actuel aurait nécessité plus de briques, en réalité

fois plus pour un mur qui aurait exatement

briques à chaque étage.
On obtinent donc en arrondissant à l'entier supèrieur
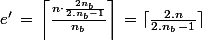
avec
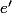
égal à 1 au rez-de-chaussée.
On peut simplifier cette expression et surtout utiliser l'arrondi à l'entier inférieur qui correspond mieux à la définition d'une valeur entière. On prendre alors en considèration

de façon à ce que l'étage commence à 0 pour l'étage le plus bas.
On obtient
}{2.n_b-1}}\right\rfloor)
où les crochets désignent l'entier

immédiatement inférieur à la valeur

et
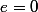
au rez-de chaussée.
Pour déterminer la position à chaque étage, il ne reste plus qu'à considérer le nombre de block (ou de double briques) qu'il reste après avoir retirer le
nombre moyen de briques (ou demi-block) de chaque étage. La position est donc le reste d'une division euclidienne par le nombre moyen de block à chaque étage:
}{2} \right ))
Mais, on peux aussi exprimer cette position en fonction de l'étage précédement calculé :
}{2}\cdot e\right)\,=\,n\,-\,\frac{e.(2n_b-1)}{2}\,=\,n-\left\lfloor{\frac{2.(n-1)}{2.n_b-1}}\right\rfloor\left(\frac{2.n_b-1}{2}\right))
Dans ce cas,

pour indiquer les positions des étages à

blocks.

pour indiquer les positions décallées (d'un demi-block) sur les étages à

blocks.
- Code: Tout sélectionner
n_b=3
n: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ...
e: 0 0 0 1 1 2 2 2 3 3 4 4 4 5 5 6 ...
p: 1 2 3 1.5 2.5 1 2 3 1.5 2.5 1 2 3 1.5 2.5 1 ...
 [/CENTER]
[/CENTER]