Comment calculer Phi ?

par **Clemou44** » 02 Jan 2013, 11:04

Bonjour, je voudrais savoir comment on calcul Phi car j'en ai besoin pour mon DM de math :)
Merci d'avance :)

par **lemec** » 02 Jan 2013, 11:07

Clemou44 a écrit:Bonjour, je voudrais savoir comment on calcul Phi car j'en ai besoin pour mon DM de math
Merci d'avance

bonjour,

mets l'enoncé

par **Kikoo <3 Bieber** » 02 Jan 2013, 11:35

Salut Clemou,

Phi est une solution de l'équation du second degré suivante :

X²-X-1=0

On arrive à cette équation dans de nombreux problèmes (des problèmes de géométrie pour la plupart) : différence entre deux nombres de la suite de Fibonacci, construction du pentagone doré, etc.

par **lemec** » 02 Jan 2013, 11:40

Kikoo <3 Bieber a écrit:Salut Clemou,

Phi est une solution de l'équation du second degré suivante :

X²-X-1=0

On arrive à cette équation dans de nombreux problèmes (des problèmes de géométrie pour la plupart) : différence entre deux nombres de la suite de Fibonacci, construction du pentagone doré, etc.

bonjour,

pas au niveau college,

par **Kikoo <3 Bieber** » 02 Jan 2013, 11:44

Pourquoi pas ? On peut essayer de montrer que le rapport d'un côté du pentagone d'or sur une de ses diagonales vaut le nombre d'or. La construction et le traitement nécessitent un peu de géométrie élémentaire, style trigonométrie, mais sont tout à fait abordables en troisième !

par **lemec** » 02 Jan 2013, 11:52

Kikoo <3 Bieber a écrit:Pourquoi pas ? On peut essayer de montrer que le rapport d'un côté du pentagone d'or sur une de ses diagonales vaut le nombre d'or. La construction et le traitement nécessitent un peu de géométrie élémentaire, style trigonométrie, mais sont tout à fait abordables en troisième !

ok mais une équation du 2nd degré ne se resouds pas en 3eme

par **lemec** » 02 Jan 2013, 11:52

Kikoo <3 Bieber a écrit:Pourquoi pas ? On peut essayer de montrer que le rapport d'un côté du pentagone d'or sur une de ses diagonales vaut le nombre d'or. La construction et le traitement nécessitent un peu de géométrie élémentaire, style trigonométrie, mais sont tout à fait abordables en troisième !

ok mais une équation du 2nd degré ne se resouds pas en 3eme,

exo sur le rectangle d'or surement

par **Clemou44** » 02 Jan 2013, 17:00

lemec a écrit:ok mais une équation du 2nd degré ne se resouds pas en 3eme,

exo sur le rectangle d'or surement

Voila, c'est sur le rectangle d'or qu'on doit calculer Phi

par **Clemou44** » 02 Jan 2013, 17:08

http://nsa31.casimages.com/img/2013/01/02/13010205081531764.jpg
C'est l'énoncé

par **chaa13** » 02 Jan 2013, 17:20

Hey !
trop Cool l'exo, il est super interressant !
Mais il te demande ou de calculer phi ?
PS: mince désolé pour l'incrustation et en plus je dois partir donc je pourrais plus répondre --'

par **Clemou44** » 02 Jan 2013, 18:03

Il nous demande de calculer Phi à l'exercice 2 petit 5 , c'est pour donner son millième ;)

par **Kikoo <3 Bieber** » 02 Jan 2013, 18:10

Ben on prend la calculatrice :dodo:

par **Clemou44** » 02 Jan 2013, 18:21

Oui mais faut détailler le calculer je pense :') Donc a la calculatrice ^^

par **Kikoo <3 Bieber** » 02 Jan 2013, 18:37

Non, moi je taperais sur ma calculatrice qui me donne un résultat approché que je tronque à mon tour au millième !

(franchement, tu connais l'expression décimale de

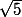
à la 4ème ou 5ème décimale ? ^^)

par **Clemou44** » 02 Jan 2013, 18:39

Non je connais pas mais après je sais que Phi sa fais environ 1.618 mais voila faut détailler le calcul de Phi !

par **Kikoo <3 Bieber** » 02 Jan 2013, 18:42

C'est marqué où que tu dois détailler le calcul ?

par **Clemou44** » 03 Jan 2013, 09:33

Mais si on doit le calculer au millième, faut bien le calculer mais sans calculatrice sinon notre prof va nous mettre comment est ce tu as fais !

Comment calculer Phi ?

Comment calculer Phi ?

Qui est en ligne