Transformer f(x) en (f(x))^i

[anthony_unac]

Au temps pour moi, la démarche ET le résultat est faux !

[anthony_unac]

Et n'a pas de sens !

[Ben314]

Bonjour,
Le calcul de (-2)^i est pourtant juste donc la démarche est juste.

J'aimerais bien savoir comment tu fait pour savoir si un calcul contenant un symbole qui n'a pas été défini précédemment est "juste" ou s'il est "faux" ?

Par exemple, si je te dit juste que j'ai envi d'étendre la notion de déterminant aux matrices rectangulaires et que je te demande si le calcul est "juste" ou "faux", tu répond quoi ?
Ta réponse m'intéresse fortement vu que moi, je ne vois vraiment pas comment je pourrais bien m'y prendre pour répondre quoi que ce soit à une question pareille...

[Ben314]

Et sinon, si on y tient, on peut donner du sens à (-2)^i en le définissant comme étant égal à exp(i.Log(-2)) où, bien sûr, il faut préciser de quelle fonction logarithme complexe on parle :

- Si on prend par exemple comme fonction Log la primitive de z->1/z définie sur C privé de la demi droite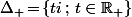 (qui est bien un ouvert simplement connexe) et telle que Log(1)=0 alors on obtient donc .

- Mais si on prend comme Log la primitive de z->1/z définie sur C privé de la demi droite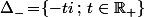 et telle que Log(1)=0 alors et donc .