Bonjour a tous,
gros problème que je n arrive pas à résoudre malgré mes recherches sur les forums...
nous organisons des olympiades avec 8 équipes.
pour cela nous avons trouvé 7 jeux.
le but : que les différentes équipes jouent à chaque jeu 1 fois et se rencontrent 1 fois sur le tournoi.
problème : je n arrive pas à construire la bonne combinaison.
même en prenant en compte que pendant que 4 équipes en rencontrent 4, 3 jeux restent en ''pause''
si quelqu'un peut m'aider ca serait super !!!!
merci d'avance
Tournoi par équipes
13 messages
- Page 1 sur 1
Re: tournoi par équipes
Hello,
Très jolie question mais qui mériterait peut-être une petite clarification ?
Je peux me fourvoyer mais la première condition impose que chaque équipe joue à chaque jeu une fois ? Si c'est le cas, la seconde condition doit être interprétée comme : chaque équipe se rencontre une fois par jeu, donc chaque équipe se rencontre sept fois sur la durée du tournoi.
mais la première condition impose que chaque équipe joue à chaque jeu une fois ? Si c'est le cas, la seconde condition doit être interprétée comme : chaque équipe se rencontre une fois par jeu, donc chaque équipe se rencontre sept fois sur la durée du tournoi.
Si ce n'est pas le cas... he bien alors chaque jeu ne devrait être joué qu'une seule fois par deux équipes. Ce qui me paraît très étrange. Je vais donc supposer que c'est le premier cas qui est le bon.
Ensuite... que cherches-tu à faire au juste ? Compter le nombre de parties à jouer ?
Peut-être rien qu'en clarifiant ça, cela t'aidera ? De mon côté, je vais compter le nombre de parties à jouer.
Chaque équipe rencontre chaque autre équipe à chaque jeu. Faisons le calcul pour un jeu, il suffira de multiplier ce nombre par 7 par après. Je sais qu'il y a des formules et tout et tout mais en combinatoire, rien ne vaut la compréhension.
L'équipe 1 rencontre les équipes 2 à 8, totalisant... 7 parties.
l'équipe 2 rencontre les équipes 3 à 8, car sa rencontre avec l'équipe 1 a déjà été prise en compte, totalisant 6 parties.
L'équipe 3 rencontre les équipes 4 à 8, etc.
Au total, il y a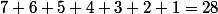 parties jouées à chaque jeu. Au total
parties jouées à chaque jeu. Au total 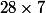 parties seront jouées pendant le tournoi.
parties seront jouées pendant le tournoi.
En espérant que même si je ne réponds pas à la question cachée, j'ai réussi à te débloquer.
- Nerra
Très jolie question mais qui mériterait peut-être une petite clarification ?
Je peux me fourvoyer
 mais la première condition impose que chaque équipe joue à chaque jeu une fois ? Si c'est le cas, la seconde condition doit être interprétée comme : chaque équipe se rencontre une fois par jeu, donc chaque équipe se rencontre sept fois sur la durée du tournoi.
mais la première condition impose que chaque équipe joue à chaque jeu une fois ? Si c'est le cas, la seconde condition doit être interprétée comme : chaque équipe se rencontre une fois par jeu, donc chaque équipe se rencontre sept fois sur la durée du tournoi.Si ce n'est pas le cas... he bien alors chaque jeu ne devrait être joué qu'une seule fois par deux équipes. Ce qui me paraît très étrange. Je vais donc supposer que c'est le premier cas qui est le bon.
Ensuite... que cherches-tu à faire au juste ? Compter le nombre de parties à jouer ?
Peut-être rien qu'en clarifiant ça, cela t'aidera ? De mon côté, je vais compter le nombre de parties à jouer.
Chaque équipe rencontre chaque autre équipe à chaque jeu. Faisons le calcul pour un jeu, il suffira de multiplier ce nombre par 7 par après. Je sais qu'il y a des formules et tout et tout mais en combinatoire, rien ne vaut la compréhension.
L'équipe 1 rencontre les équipes 2 à 8, totalisant... 7 parties.
l'équipe 2 rencontre les équipes 3 à 8, car sa rencontre avec l'équipe 1 a déjà été prise en compte, totalisant 6 parties.
L'équipe 3 rencontre les équipes 4 à 8, etc.
Au total, il y a
En espérant que même si je ne réponds pas à la question cachée, j'ai réussi à te débloquer.
- Nerra
Re: tournoi par équipes
Slt nerra
Lenonce est assez clair, imagine que tas 7jours, chaque jour tu lances 4matches ... sur le jeu du jour, ca tombe bien yen a 7 aussi.
A lissue des 7jours ttes les equipes, si possible, doivent avoir affronté ttes les autres.
Il fait dire qui joue contre qui pr chaque jour.
On peut, mais ya certainement mieux, modeliser ainsi:
8eq numerotees de 0 a 7.
Ya 28 paires possibles (paire== doublon dequipe)
On pose le premier jour de maniere arbitraire(ex 07,12,34,56) Il reste un pool de 24 paires
Pr eliminer les combi inutiles:
Sur un jour, pas une equipe ds deux paires.
Qd on pioche unr paire, on lenleve du pool disponible puis... on espere que ca termine,
Faute davoir un cerveau pr reflechir plus
Lenonce est assez clair, imagine que tas 7jours, chaque jour tu lances 4matches ... sur le jeu du jour, ca tombe bien yen a 7 aussi.
A lissue des 7jours ttes les equipes, si possible, doivent avoir affronté ttes les autres.
Il fait dire qui joue contre qui pr chaque jour.
On peut, mais ya certainement mieux, modeliser ainsi:
8eq numerotees de 0 a 7.
Ya 28 paires possibles (paire== doublon dequipe)
On pose le premier jour de maniere arbitraire(ex 07,12,34,56) Il reste un pool de 24 paires
Pr eliminer les combi inutiles:
Sur un jour, pas une equipe ds deux paires.
Qd on pioche unr paire, on lenleve du pool disponible puis... on espere que ca termine,
Faute davoir un cerveau pr reflechir plus

la vie est une fête 
Re: tournoi par équipes
hello!
merci de vos réponses! en effet vous m'avez bien compris
effectivement j'ai fait toutes les combinaisons possibles de challenge par équipe (1-2...1-8;2-3...2-8;3-4...3-8 etc jusqu’à 7-8 puisqu'ils rencontrent déjà les autres équipes avant)
donc cela fait 28 matchs en tout, car par exemple :
l'équipe 1 rencontre la 2 au jeu A mais elles ne jouent ce jeu qu'une fois
l'équipe 1 rencontrera la 3 au jeu B
il faut donc prendre en compte que 8 équipes s'affrontant, seuls 7 jeux sont nécessaires puisqu'on ne s'affronte pas soi même
a chaque tour il y a 4 matchs, donc 3 jeux sont sans personne.
j'ai essayé fatal_error de me servir du carré gréco latin que tu avais donné sur un autre forum de ce type il y a quelques années mais impossible de le mettre en pratique...
je désespère de croire qu'il y a une solution...
merci de vos réponses! en effet vous m'avez bien compris
effectivement j'ai fait toutes les combinaisons possibles de challenge par équipe (1-2...1-8;2-3...2-8;3-4...3-8 etc jusqu’à 7-8 puisqu'ils rencontrent déjà les autres équipes avant)
donc cela fait 28 matchs en tout, car par exemple :
l'équipe 1 rencontre la 2 au jeu A mais elles ne jouent ce jeu qu'une fois
l'équipe 1 rencontrera la 3 au jeu B
il faut donc prendre en compte que 8 équipes s'affrontant, seuls 7 jeux sont nécessaires puisqu'on ne s'affronte pas soi même
a chaque tour il y a 4 matchs, donc 3 jeux sont sans personne.
j'ai essayé fatal_error de me servir du carré gréco latin que tu avais donné sur un autre forum de ce type il y a quelques années mais impossible de le mettre en pratique...
je désespère de croire qu'il y a une solution...

Re: tournoi par équipes
je suis à la bourre... je pourrai détailler si nécessaire
voici une composition
code
edit: corrigé marche pour N pair jusqu'à 20
voici une composition
- Code: Tout sélectionner
(0,1) (2,3) (4,5) (6,7)
(0,2) (1,3) (4,6) (5,7)
(0,3) (1,2) (4,7) (5,6)
(0,4) (1,5) (2,6) (3,7)
(0,5) (1,4) (2,7) (3,6)
(0,6) (1,7) (2,4) (3,5)
(0,7) (2,5) (1,6) (3,4)
code
edit: corrigé marche pour N pair jusqu'à 20
- Code: Tout sélectionner
function runDay(days, poules, depth, mPerDay){
if(depth == 0){
return JSON.parse(JSON.stringify(days));
}
return fillDay(days, poules, depth, mPerDay, [], 0, 0);
}
function fillDay(days, poules, depth, mPerDay, day, binaryDay, pouleIndex){
if(day.length == mPerDay){
days.push(day);
var res = runDay(days, poules, depth-1, mPerDay);
days.pop();
return res;
}
for(var i = pouleIndex, lp=poules.length; i< lp; ++i){
var poule = poules[i];
var res = binaryDay & poule
if(res){
continue;
}
var oldDay = binaryDay;
poules.splice(i,1);
day.push(poule);
var res = fillDay(days, poules, depth, mPerDay, day, binaryDay|poule, pouleIndex);
day.pop();
poules.splice(i,0,poule);
binaryDay = oldDay;
if(res){
return res;
}
}
return false;
}
//poule: byte
function makePoule(i,j){
var p = 0;
p = p | 2 << i;//offset 0
p = p | 2 << j;
return p;
}
function bString(p){
var arr = [];
for(var i = 0;i<N;++i){
if(p & 2 << i){
arr.push(i);
}
}
return '('+arr.join(',')+')';
}
function solutionToString(days){
if(days==false){
return 'no sol';
}
return days.map(d=>{
return d.map(bString).join(' ');
}).join('\n');
}
function checkSolution(s){
var dic = {};
return s.every(d=>{
var binaryDay = 0;
for(var i = 0;i<d.length; ++i){
var p = d[i];
if(dic[p]){
return false;
}
dic[p] = 1;
var res = binaryDay & p
if(res){
return false;
}
binaryDay |= p;
}
return true;
});
}
var N = 8;
var poules = [];
for(var i = 0;i<N;++i){
for(var j = i+1;j<N;++j){
poules.push(makePoule(i,j));
}
}
console.log(solutionToString(runDay([], poules, N-1, N/2)));
la vie est une fête 
Re: tournoi par équipes
edit:
il suffisait de
var res = fillDay(days, poules, depth, day, binaryDay|poule, pouleIndex);
au lieu de
var res = fillDay(days, poules, depth, day, binaryDay|poule, pouleIndex+1);
(splice modifie dejà le tableau..)
il suffisait de
var res = fillDay(days, poules, depth, day, binaryDay|poule, pouleIndex);
au lieu de
var res = fillDay(days, poules, depth, day, binaryDay|poule, pouleIndex+1);
(splice modifie dejà le tableau..)
la vie est une fête 
Re: tournoi par équipes
vu que ca semble marcher pour tt n pair, on peut observer un certain pattern sur la construction du tableau
on peut intuiter qu'il y a un algo plus séduisant que le brute force (_(
on peut intuiter qu'il y a un algo plus séduisant que le brute force (_(
la vie est une fête 
Re: tournoi par équipes
désolée pour la réponse tardive...
merci fatal mais si je suis ton tableau avec les chiffres, soit une équipe reste tout le temps coincé sur le même jeu, soit elle doit affronter toutes les autres équipes en même temps :'D
Donc soit j'ai raté un épisode, soit je devrais trouver une autre solution !!
merci fatal mais si je suis ton tableau avec les chiffres, soit une équipe reste tout le temps coincé sur le même jeu, soit elle doit affronter toutes les autres équipes en même temps :'D
Donc soit j'ai raté un épisode, soit je devrais trouver une autre solution !!
Re: tournoi par équipes
Bonjour,
jeu 1 : équipes 1-2, 3-4, 5-6, 7-8
jeu 2 : équipes 1-3, 2-4, 5-7, 6-8
jeu 3 : équipes 1-4, 2-3, 5-8, 6-7
jeu 4 : équipes 1-5, 2-6, 3-7, 4-8
jeu 5 : équipes 1-6, 2-7, 3-8, 4-5
jeu 6 : équipes 1-7, 2-8, 3-5, 4-6
jeu 7 : équipes 1-8, 2-5, 3-6, 4-7
Sauf erreur et si j'ai bien compris.
jeu 1 : équipes 1-2, 3-4, 5-6, 7-8
jeu 2 : équipes 1-3, 2-4, 5-7, 6-8
jeu 3 : équipes 1-4, 2-3, 5-8, 6-7
jeu 4 : équipes 1-5, 2-6, 3-7, 4-8
jeu 5 : équipes 1-6, 2-7, 3-8, 4-5
jeu 6 : équipes 1-7, 2-8, 3-5, 4-6
jeu 7 : équipes 1-8, 2-5, 3-6, 4-7
Sauf erreur et si j'ai bien compris.
Re: tournoi par équipes
hello!
c'est presque ca!
sauf qu'il faut imaginer que les jeux se jouent en même temps (de 1 a 7, donc évidemment 3 jeux en pause pendant une manche...) et c'est la que ca se complique.. l'equipe 1 ne peut pas affronter la 2 sur le jeu 1 en meme temps qu'elle afronte la 3 sur le jeu 2...
c'est presque ca!
sauf qu'il faut imaginer que les jeux se jouent en même temps (de 1 a 7, donc évidemment 3 jeux en pause pendant une manche...) et c'est la que ca se complique.. l'equipe 1 ne peut pas affronter la 2 sur le jeu 1 en meme temps qu'elle afronte la 3 sur le jeu 2...
Re: tournoi par équipes
Bonsoir,
Ah. La contrainte, c'est de pouvoir jouer en même temps, et chaque équipe doit se rencontrer sur chaque jeu.
Dans ce cas, on fait tourner les équipes sur chaque jeu de façon que les jeux puissent avoir lieu en même temps ? :
1er round : jeu 1 : 1-2, jeu 2 : 3-4, jeu 3 : 5-6, jeu 4 : 7-8
2ème round : jeu 1 : 3-4, jeu 2 : 5-6, jeu 3 : 7-8, jeu 4 : 1-2
etc...
en mélangeant les rounds pour que les mêmes équipes ne se rencontrent pas à la suite.
Ah. La contrainte, c'est de pouvoir jouer en même temps, et chaque équipe doit se rencontrer sur chaque jeu.
Dans ce cas, on fait tourner les équipes sur chaque jeu de façon que les jeux puissent avoir lieu en même temps ? :
1er round : jeu 1 : 1-2, jeu 2 : 3-4, jeu 3 : 5-6, jeu 4 : 7-8
2ème round : jeu 1 : 3-4, jeu 2 : 5-6, jeu 3 : 7-8, jeu 4 : 1-2
etc...
en mélangeant les rounds pour que les mêmes équipes ne se rencontrent pas à la suite.
Re: tournoi par équipes
Bonjour
Jour 1 : jeuA 1-8 jeuE 2-6 jeuB 3-4 jeuC 5-7
Jour 2 : jeuD 1-5 jeuF 2-4 jeuE 7-8 jeuA 3-6
Jour 3 : jeuG 1-2 jeuB 8-6 jeuA 4-5 jeuD 3-7
Jour 4 : jeuF 1-3 jeuC 4-8 jeuG 5-6 jeuA 2-7
Jour 5 : jeuE 1-4 jeuB 2-5 jeuG 3-8 jeuF 6-7
Jour 6 : jeuC 1-6 jeuD 2-8 jeuE 3-5 jeuG 4-7
Jour 7 : jeu B 1-7 jeuC 2-3 jeuF 5-8 jeuD 4-6
Sauf erreur, ça a marché.
Jour 1 : jeuA 1-8 jeuE 2-6 jeuB 3-4 jeuC 5-7
Jour 2 : jeuD 1-5 jeuF 2-4 jeuE 7-8 jeuA 3-6
Jour 3 : jeuG 1-2 jeuB 8-6 jeuA 4-5 jeuD 3-7
Jour 4 : jeuF 1-3 jeuC 4-8 jeuG 5-6 jeuA 2-7
Jour 5 : jeuE 1-4 jeuB 2-5 jeuG 3-8 jeuF 6-7
Jour 6 : jeuC 1-6 jeuD 2-8 jeuE 3-5 jeuG 4-7
Jour 7 : jeu B 1-7 jeuC 2-3 jeuF 5-8 jeuD 4-6
Sauf erreur, ça a marché.
Re: tournoi par équipes
MERCI MERCI MERCI Wsc !!!!!
enfin ça a marché et on a réussi grâce a toi! merci encore de ton aide !!!
Maintenant y a plus qu'a jouer !!
enfin ça a marché et on a réussi grâce a toi! merci encore de ton aide !!!
Maintenant y a plus qu'a jouer !!
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
