2 questions sur les nombres complexes
15 messages
- Page 1 sur 1
2 questions sur les nombres complexes
1) Pourquoi donne ton le meme nom (nombre complexe) a
Z=Ro*e^(i*theta) et a W=Ro*(cos theta+ sin theta)
Il me semble quon a perdu de linformation en passant de Z a W ,par exemple si theta=6*Pi+x
2) Dautre part pourquoi dit on quon ne peut pas ordonner le corps des complexes
Si je prend comme relation dordre leurs modules, et si leurs modules est egale alors on compare leurs arguments ?, dans le cas ou je definis un nombre complexe comme Z=Ro*e^(i*theta)
Il me semble que cest alors un ensemble ordonné ?.
Z=Ro*e^(i*theta) et a W=Ro*(cos theta+ sin theta)
Il me semble quon a perdu de linformation en passant de Z a W ,par exemple si theta=6*Pi+x
2) Dautre part pourquoi dit on quon ne peut pas ordonner le corps des complexes
Si je prend comme relation dordre leurs modules, et si leurs modules est egale alors on compare leurs arguments ?, dans le cas ou je definis un nombre complexe comme Z=Ro*e^(i*theta)
Il me semble que cest alors un ensemble ordonné ?.
si j'avais su j'aurais pas venu.
Bonjour, il y a égalité entre les nombres Re^(it) et R(cos t + i sint). Il n'y a pas d'information perdue ou quoi que ce soit du genre, c'est une égalité. Si t = 6pi + x on a Re^(it) = R(cos t + i sint) = Re^(ix) = R(cos x + i sin x).
Pour ta deuxième question, ça peut être considéré comme un abus de langage. Tu as tout à fait raison en disant qu'on peut ordonner C. L'ordre que tu donnes (auquel il faudrait juste ajouter une condition sur les arguments du genre "argument principal" pour pouvoir les comparer) est valide, on pourrait aussi comparer les parties réelle et imaginaire, ou penser à un ordre plus exotique. En revanche, on ne peut pas ordonner C en tant que corps. Sous-entendu : on ne peut pas le munir d'un ordre total qui respecte sa structure de corps, c'est-à-dire d'un ordre < qui vérifie les propriétés "pour tous complexes a, b et c, a < b implique a+c < b+c" et "pour tous complexes a et b, a > 0 et b > 0 implique ab > 0". Sans ces propriétés, l'utilisation d'un ordre perd énormément de son intérêt.
Pour ta deuxième question, ça peut être considéré comme un abus de langage. Tu as tout à fait raison en disant qu'on peut ordonner C. L'ordre que tu donnes (auquel il faudrait juste ajouter une condition sur les arguments du genre "argument principal" pour pouvoir les comparer) est valide, on pourrait aussi comparer les parties réelle et imaginaire, ou penser à un ordre plus exotique. En revanche, on ne peut pas ordonner C en tant que corps. Sous-entendu : on ne peut pas le munir d'un ordre total qui respecte sa structure de corps, c'est-à-dire d'un ordre < qui vérifie les propriétés "pour tous complexes a, b et c, a < b implique a+c < b+c" et "pour tous complexes a et b, a > 0 et b > 0 implique ab > 0". Sans ces propriétés, l'utilisation d'un ordre perd énormément de son intérêt.
Bonjour.
1)Non, on n'a pas perdu d'information;+isin(\theta)) .
.
2)Ca ressemble à l'ordre lexicographique.
Par contre, il est impossible de définir sur C une relation de corps totalement ordonné. On peut y définir des relations d'ordre, mais elles seront soit totales, soit compatibles avec sa structure de corps.
EDIT: grillé
1)Non, on n'a pas perdu d'information;
2)Ca ressemble à l'ordre lexicographique.
Par contre, il est impossible de définir sur C une relation de corps totalement ordonné. On peut y définir des relations d'ordre, mais elles seront soit totales, soit compatibles avec sa structure de corps.
EDIT: grillé
Pour commencer, un nombre en 3D ou en 2D ça veut rien dire. Et si jamais tu veux associer une dimension à C, ce ne sera certainement pas 3.
Pour ce qui est de ton "test", ce que tu as écrit ne veut rien dire non plus... En le formulant correctement, tu nous donnes un nombre complexe (5 + 3i) et tu nous demandes de retrouver, parmi l'infinité d'arguments qu'il admet, celui auquel tu penses...
On peut tous faire des "tests" comme ça sans avoir besoin de nombres complexes : je pense à deux nombres réels dont le produit fait 20, quels sont ces deux nombres ? Tu ne peux évidemment pas deviner puisqu'il y a une infinité de couples de réels dont le produit fait 20. Ce que tu dis toi en gros c'est que 20 n'est pas égal à 5*4, parce que l'écriture 5*4 "donne plus d'information"... Mais que tu l'écrives 5*4, 10*2, 120/6 ou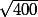 , 20 c'est 20 et pas un autre nombre.
, 20 c'est 20 et pas un autre nombre.
Pour ce qui est de ton "test", ce que tu as écrit ne veut rien dire non plus... En le formulant correctement, tu nous donnes un nombre complexe (5 + 3i) et tu nous demandes de retrouver, parmi l'infinité d'arguments qu'il admet, celui auquel tu penses...
On peut tous faire des "tests" comme ça sans avoir besoin de nombres complexes : je pense à deux nombres réels dont le produit fait 20, quels sont ces deux nombres ? Tu ne peux évidemment pas deviner puisqu'il y a une infinité de couples de réels dont le produit fait 20. Ce que tu dis toi en gros c'est que 20 n'est pas égal à 5*4, parce que l'écriture 5*4 "donne plus d'information"... Mais que tu l'écrives 5*4, 10*2, 120/6 ou
Skullkid a écrit:Pour commencer, un nombre en 3D ou en 2D ça veut rien dire. Et si jamais tu veux associer une dimension à C, ce ne sera certainement pas 3.
Pour ce qui est de ton "test", ce que tu as écrit ne veut rien dire non plus... En le formulant correctement, tu nous donnes un nombre complexe (5 + 3i) et tu nous demandes de retrouver, parmi l'infinité d'arguments qu'il admet, celui auquel tu penses...
On peut tous faire des "tests" comme ça sans avoir besoin de nombres complexes : je pense à deux nombres réels dont le produit fait 20, quels sont ces deux nombres ? Tu ne peux évidemment pas deviner puisqu'il y a une infinité de couples de réels dont le produit fait 20. Ce que tu dis toi en gros c'est que 20 n'est pas égal à 5*4, parce que l'écriture 5*4 "donne plus d'information"... Mais que tu l'écrives 5*4, 10*2, 120/6 ou, 20 c'est 20 et pas un autre nombre.
Ce que je voulais dire cest quau nombre Z=Ro*e^(i*theta)
On peut associer un point dans lespace , le troisieme axe etant gradué en nombre de 2*pi, et quand on lecrit sous la forme W=Ro*(cos theta+ i*sin theta) on ne peut lui associer quun point sur le plan.
dans ton cas
« c'est que 20 n'est pas égal à 5*4, parce que l'écriture 5*4 "donne plus d'information"... Mais que tu l'écrives 5*4, 10*2, 120/6 ou , 20 c'est 20 et pas un autre nombre. »
cest toujours le meme point sur la droite
si j'avais su j'aurais pas venu.
ortollj a écrit:Ce que je voulais dire cest quau nombre Z=Ro*e^(i*theta)
On peut associer un point dans lespace , le troisieme axe etant gradué en nombre de 2*pi, et quand on lecrit sous la forme W=Ro*(cos theta+ i*sin theta) on ne peut lui associer quun point sur le plan.
Non, le nombre complexe 1 est égal au nombre complexe e^(2 i pi) qui est égal au nombre complexe e^(2548 i pi). Un nombre complexe a une infinité d'arguments et l'ensemble des arguments de e^(2 i pi) est exactement le même que celui de e^(2548 i pi).
Pour revenir à tes 3 axes, avec la représentation que tu proposes, un nombre complexe n'est pas représenté par un point dans l'espace mais par une "droite" parallèle à ton troisième axe (ce n'est pas vraiment une droite puisque tu gradues ton troisième axe avec des entiers uniquement). Et 1 est représenté par la même droite que e^(2 i pi).
ortollj a écrit:1) Pourquoi donne ton le meme nom (nombre complexe) a
Z=Ro*e^(i*theta) et a W=Ro*(cos theta+ sin theta)
Il me semble quon a perdu de linformation en passant de Z a W ,par exemple si theta=6*Pi+x
Ca vient des développements en séries entières. Quand on developpe
J'ai lu ça sur je ne sais plus quel bouquin. Je le réemprunterais à la B.U et je te filerais la référence si tu veux.
Cryptocatron-11 a écrit:Ca vient des développements en séries entières. Quand on developpeen somme de polynome, on retrouve la même chose que quand on développe
.
J'ai lu ça sur je ne sais plus quel bouquin. Je le réemprunterais à la B.U et je te filerais la référence si tu veux.
merci Cryptocatron
j'ai trouvé la demonstration de la formule d'Euler ici.
http://fr.wikipedia.org/wiki/Formule_d'Euler
mais il ya beaucoup de questions que je me pose sur cette representation.
par exemple Z=Ro*e^(i*(2*Pi*n)+x) avec 0 <x<2*Pi et n E Naturel
si je multiplie par -1 j'obtiens -Z= Y=R0*e^(i*(2*Pi*(n+0,5))+x) en applicant cette formule, et d'un autre coté que signifie un module negatif ? c'est une histoire de fou !.
si j'avais su j'aurais pas venu.
ortollj a écrit:merci Cryptocatron
j'ai trouvé la demonstration de la formule d'Euler ici.
http://fr.wikipedia.org/wiki/Formule_d'Euler
mais il ya beaucoup de questions que je me pose sur cette representation.
par exemple Z=Ro*e^(i*(2*Pi*n)+x) avec 0 <x<2*Pi et n E Naturel
si je multiplie par -1 j'obtiens -Z= Y=R0*e^(i*(2*Pi*(n+0,5))+x) en applicant cette formule, et d'un autre coté que signifie un module negatif ? c'est une histoire de fou !.
Le module d'un nombre complexe est un réel positif, un module négatif ça n'existe pas.
Ensuite, je me répète, mais e^(2 i n pi) = 1 donc le ton nombre Z ça n'est ni plus ni moins que R0*e^(ix). Si tu le multiplies par -1 tu obtiens Y = -R0*e^(ix) mais ça ne veut pas dire que le module de Y est -R0 ! Le module de Y c'est R0 et un de ses arguments est x + pi.
SI z = r*e^(it) avec r un réel positif et t un réel, ALORS r est le module de z et t est un argument de z.
Ton Y on peut le réécrire Y = -R0*e^(ix) = R0*e^(i pi)*e^(ix) = R0*e^(i(x+pi)). Une fois qu'on a mis Y sous cette forme (réel positif multiplié par l'exponentielle d'un imaginaire pur) on peut "voir" le module et un argument de Y.
Naturellement, Y est aussi égal à R0*e^(i(x+3pi)), donc x+3pi est aussi un argument de Y. Les arguments de Y sont tous les x + (2k+1)pi, avec k entier relatif.
La représentation d'un complexe par son module et un de ses arguments c'est la même chose que les coordonnées polaires en géométrie : on repère un point M par la distance OM qui le sépare de l'origine (un réel positif) et une mesure de l'angle orienté
ok merci Skullkid(ces nombres complexes n'arretent pas de me torturer le cervelet !).
regardez la video , c'est impressionant.
http://images.math.cnrs.fr/Mandelbulb.html
regardez la video , c'est impressionant.
http://images.math.cnrs.fr/Mandelbulb.html
si j'avais su j'aurais pas venu.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
