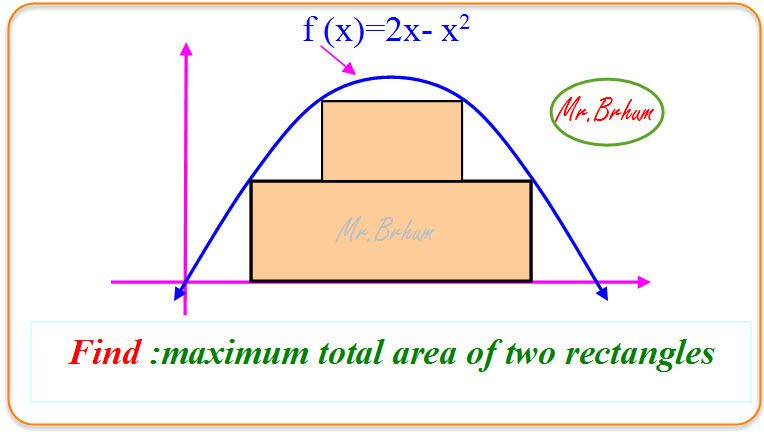
Maximum total area
3 messages
- Page 1 sur 1
Salut,
=1-t^2=f(1+t)) : La parabole est symétrique par rapport à la droite x=1.
: La parabole est symétrique par rapport à la droite x=1.
Si la base du premier rectangle (en bas) est où
où  alors son aire est
alors son aire est
=2t(1-t^2))
Si la base du deuxième rectangle est où
où  ) alors son aire est
) alors son aire est
-f(1-t)\big)=2s(t^2-s^2))
Pour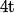 fixé,
fixé,  est maximum lorsque
est maximum lorsque  (dérivée) c'est à dire
(dérivée) c'est à dire  et
et 
On a alorst^3) qui est maximum lorsque
qui est maximum lorsque t^2=0) (dérivée) c'est à dire
(dérivée) c'est à dire
 et
et  (pourri)
(pourri)
Si la base du premier rectangle (en bas) est
Si la base du deuxième rectangle est
Pour
On a alors
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En fait, il y a une façon plus simple de mener le calcul.
Pour simplifier, on commence par centrer le repère en (1,1) de façon à ce que l'équation de la courbe soit simplement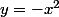 qui est stable par toute affinité de la forme
qui est stable par toute affinité de la forme \mapsto(ax,a^2y)) qui a le bon gout de multiplier les aires par
qui a le bon gout de multiplier les aires par 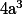 .
.
Notons alors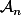 l'aire maximale que l'on peut obtenir à l'aide de
l'aire maximale que l'on peut obtenir à l'aide de  rectangles, celui le plus bas étant "posé" sur la droite
rectangles, celui le plus bas étant "posé" sur la droite 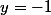 .
.
Grâce à l'affinité çi dessus, on en déduit que l'aire maximale que l'on peut obtenir à l'aide de rectangles, celui le plus bas étant "posé" sur la droite
rectangles, celui le plus bas étant "posé" sur la droite  (image de
(image de 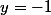 par l'affinité) est
par l'affinité) est  .
.
Donc, lorsque l'on cherche à déterminer , si le rectangle le plus bas a pour base
, si le rectangle le plus bas a pour base 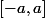 (
(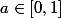 ) alors le plus bas des
) alors le plus bas des  autres sera "posé" sur la droite
autres sera "posé" sur la droite  donc la somme des aires de ces
donc la somme des aires de ces  rectangles sera, au maximum, de
rectangles sera, au maximum, de  .
.
Si on ajoute l'aire du premier rectangle, on obtient+a^3{\mathcal A_n}=2a-(2-{\mathcal A_n})a^3) qui est maximum lorsque
qui est maximum lorsque a^2=0) (dérivée) c'est à dire
(dérivée) c'est à dire }}) ce qui donne
ce qui donne
}}\big(2-\frac{2}{3}\big)=\frac{8}{3\sqrt{6(2-{\mathcal A_n})}\ \ \)
Comme , on a
, on a  et
et \sqrt{9-2\sqrt{3}}}{69})
Remarque : On peut vérifier que tend vers
tend vers 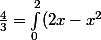\,dx)
Pour simplifier, on commence par centrer le repère en (1,1) de façon à ce que l'équation de la courbe soit simplement
Notons alors
Grâce à l'affinité çi dessus, on en déduit que l'aire maximale que l'on peut obtenir à l'aide de
Donc, lorsque l'on cherche à déterminer
Si on ajoute l'aire du premier rectangle, on obtient
Comme
Remarque : On peut vérifier que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
