Intrigant !

[Anonyme]

Je voudrais vous montrer un petit truc intrigant que j'ai trouvé, qui est vraiment accessible à tout le monde, je pense qu'à partir de la quatrième et en se renseignant sur la factorielle on peut y arriver.

Prenons tout d'abord les carrés de nombres entiers.

1
4
9
16
25
36

Maintenant faisons leur différence

1 --> 4-1 = 3 --> 5-3=2
4 --> 9-4=5 --> 7-5=2
9 --> 16-9=7 --> 9-7=2
16 --> 25-16=9 --> 11-9=2
25 --> 36-25=11
36

On retombe toujours sur 2. Cela marche pour l'ensemble des carrés de nombres entiers.

Faisons le maintenant avec la puissance 3.

1 --> 8-1=7 --> 19-7 =12 --> 18-12=6
8 --> 27-8=19 --> 37-19 = 18 --> 21-18=6
27 --> 64-27=37 --> 61-37=24
64 --> 125-64=61
125

On retombe sur 6.

Ecoutez bien : Le nombre qui ressort à la fin de chaque suite de différences de nombres élevés à la puissance X est la factorielle de X.

J'ai essayé au brouillon jusqu'à la puissance de 6, ça marche, bien sûr à chaque fois il faut ajouter une étape pour retomber sur un même nombre, et qui en plus correspond à la factorielle de la puissance.

Voilà si vous aviez une démonstration, ce serairt bien de la poster, mais je risque de ne pas la comprendre car je n'ai qu'un niveau de 1°S. Mon prof de maths m'a montré le début vite fait, mais j'ai pas compris. En fait il prenait la formule de (a+1)^n (que l'on voit en terminale), et il montrait qu'on retombait sur un nombre constant en faisant la différence avec a^n, enfin au fur et à mesure des étapes les puissances s'affaiblissent jusqu'à laisser uniquement des nombres réels, par contre il savait pas pourquoi ça tombait sur la factorielle.

J'espère ne pas avoir été incompréhensible, merci de m'aider ! :id:

[Timothé Lefebvre]

Bonjour,

comme toi j'avais déjà trouvé une petite chose comme ça sur les factorielles. Je n'ai pas gardé le papier sur lequel j'avais fais ça mais il me semble me rappeler que j'avais étudier la différence des factorielles des nombres de 1 à 100 pour finalement me rendre compte que le phénomène que j'avais "découvert" pouvait se traduire avec une simple identité remarquable vue en troisième !

[Bebs]

Bien vu, mais la même remarque a été faite il y a quelque jours...
ICI

[skilveg]

Oui, mais seulement pour les carrés, pas pour les puissances -ièmes.

Il y a une façon de voir que l'on aboutit toujours au même nombre grâce aux polynômes. C'est sans doute ce que t'a expliqué ton prof. Tu pars du polynôme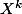 , qui représente ce qu'il y a sur la première colonne, et tu calcules , que l'on va noter (si est un polynôme, on note parfois ). Le polynôme correspond à la deuxième colonne. Et on continue: la troisième colonne, c'est , et ainsi de suite.

Maintenant, appliquer à un polynôme diminue son degré de : si , alors va être égal à qui a le même terme de degré que (les points de suspension sont des termes de degré 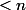). Donc la différence 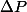n'a pas de terme de degré .

Par récurrence, si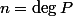 , le degré de va être 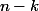. Au bout de la suite, au -ième terme, est constant. En particulier, est un polynôme constant; mais ses valeurs sur les entiers positifs sont exactement les nombres de la -ième colonne de ton tableau. Donc tous les nombres de la colonne sont égaux.

Bon, ça, c'est une chose... Mais est-ce que quelqu'un ici est capable de prouver que ? :hein:

[ffpower]

Par reccurence...
ou P est de degré n-2,or par reccurence et ,le resultat s en deduit..

[skilveg]

Et bam! Merci, ça m'a l'air bon...

NB au passage: de mon côté, j'avais calculé brutalement pour tous . Du coup ça donne la formule étrange
[CENTER]

[/CENTER]
pour tout entier naturel :doute:

[Anonyme]

Désolé j'ai pas tout compris :doh:

[miikou]

n² - (n-1)² = 2n+1
(n-1)²-(n-2)² = 2n-1 donc la difference fait 2 ( 2n+1 - ( 2n-1 )). miracle :D

[Anonyme]

Ca j'avais compris, mais tu ne le fais que pour le carré sans généraliser avec toutes les puissances et tu ne montres pas qu'il s'agit de la factorielle de la puissance.

[skilveg]

Désolé j'ai pas tout compris :doh:

`A mon baratin ou à autre chose? `A quel endroit coinces-tu?