Inégalités
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 24 Oct 2011, 21:51
par Jota Be » 24 Oct 2011, 21:51
Bonsoir à tous et à toutes.
Je me suis mis aux inégalités il y a peu et viens de commencer Cauchy-Scwharz.
J'ai compris le principe mais ne sais pas trop comment appliquer.
soit a, b et c des réels.
Montrer que

Voilà, dans la correction, je vois qu'il faut transformer l'écriture du membre de gauche en un produit mais je ne vois vraiment pas comment on arrive de

à
\bigg( \frac{ 1 }{ a+b }+ \frac{ 1 }{ b+c }+ \frac{ 1 }{ a+c }\bigg) \geq \frac{ 9 }{ 2 })
a part rajouter 3
Merci d'avance de m'aider à comprendre mieux.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 24 Oct 2011, 23:46
par SaintAmand » 24 Oct 2011, 23:46
Bonsoir,
Jota Be a écrit:je ne vois vraiment pas comment on arrive de

à
\bigg( \frac{ 1 }{ a+b }+ \frac{ 1 }{ b+c }+ \frac{ 1 }{ a+c }\bigg) \geq \frac{ 9 }{ 2 })
a part rajouter 3
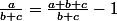
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 25 Oct 2011, 11:20
par Jota Be » 25 Oct 2011, 11:20
Merci beaucoup SaintAmand!
Malheureusement, je n'ai pas encore les réflexes.
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 25 Oct 2011, 11:36
par Bony » 25 Oct 2011, 11:36
l'énoncé est faux
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 25 Oct 2011, 12:15
par SaintAmand » 25 Oct 2011, 12:15
Bony a écrit:l'énoncé est faux
Oui, il faut prendre a,b,c réels strictement positifs.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 25 Oct 2011, 13:33
par Olympus » 25 Oct 2011, 13:33
Pour montrer ton inégalité ( Inégalité de Nesbitt ), tu peux aussi prouver que
})
:happy2:
EDIT : bien sûr en prenant en compte la remarque de SaintAmand.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 25 Oct 2011, 13:59
par SaintAmand » 25 Oct 2011, 13:59
Olympus a écrit:Pour montrer ton inégalité ( Inégalité de Nesbitt ), tu peux aussi prouver que
})
:happy2:
.
Piououou... Ma préférence va à l'IAG.
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 25 Oct 2011, 15:05
par Jota Be » 25 Oct 2011, 15:05
oui oui merci pour vos remarques, j'avais oublié de marquer que ce sont des réels positifs !
Comment en arrive-t-on à la Olympus ?!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
