Inégalités de concentration (Hoeffding)

[Luc]

Bonjour à tous,

j'ouvre un fil, mais c'est en réponse à une question que j'avais posée lors d'une des (longues) discussions sur les probabilités qui avait eu lieu sur ce forum.

Le problème était de savoir si une v.a. pouvait s'écarter beaucoup de sa moyenne ou pas. Pour pouvoir reconnaitre des "vrais aléatoires" de séries trafiquées.
Il me semble qu'il y a un résultat intéressant à ce sujet : l'inégalité de Hoeffding
http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_Hoeffding

Si on lance une pièce équilibrée 100 fois, la probabilité d'obtenir plus de 60 piles est inférieure à 0,14.

[Sylviel]

Attention, on ne regarde pas une réalisation de la variable pour dire si oui ou non elle peut s'éloigner de son espérance (ceci ne dépend que de la loi choisie, et pour une loi normale par exemple la distance à son espérance peut être aussi grande que l'on veut avec probabilité positive).

En revanche si on regarde la moyenne empirique (ou la somme, ça revient au même) et qu'on la compare à la moyenne théorique (l'espérance) on a quelques résultats dont cette inégalité. Ce qui est intéressant ici (par rapport au TCL) c'est que l'inégalité est vrai pour tout n, et non asymptotiquement...

P.S : @Luc je sais bien que tu ne fais pas la confusion mais vu ce que l'on a pu voir écrit sur le forum autant être précis :zen:

[adrien69]

Tiens j'ai eu ça en examen je pense !

[Luc]

Je suis en train de faire un exercice du style "majoration du théorème des grandes déviations", et j'aurais besoin d'une aide/vérification.

On considère une suite de v.a. i.i.d. On suppose que est bornée, non constante, de moyenne .
On cherche une majoration exponentielle de la probabilité que l'écart entre l'estimateur et dépasse .
On note la transformée de Laplace de .

1. Montrer que est C infinie, calculer ses dérivées (OK)
2. Montrer que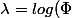 est convexe. (OK, penser à Cauchy-Schwarz). Vérifier que (OK)
3. On considère la transformée de Legendre de , notée , définie pour 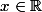par
Montrer que I est convexe, positive, et nulle en m.
(OK, mais je ne vois pas pourquoi I serait définie sur a priori, même si ce n'est pas important pour la suite).
4. Montrer la majoration
pour .

C'est là que je bloque. Peut-être faut-il utiliser une inégalité classique (Chebychev, convexité)?
EDIT : J'ai trouvé, en démontrant d'abord le résultat pour n=1, puis en l'appliquant à la variable aléatoire , et en utilisant l'indépendance. Je pense que cette méthode (n=1, puis n quelconque en utilisant l'indépendance) est assez générale.

En déduire que
Je trouve l'inégalité dans le mauvais sens quand j'applique la définition de I...

Remarquer que (OK par convexité).

5. Montrer que
OK en utilisant la définition de l'inf + un argument de symétrie.

6. Calcul explicite de la majoration exponentielle quand X est une Bernoulli de paramètre p

En utilisant la convexité de I, je trouve .
Si on est pas astucieux dans les calculs ça peut devenir assez horrible... mais il suffit d'un DL d'ordre 1+utilisation de la convexité.

Reste à comparer la majoration obtenue avec celle de la règle d'or de Bernoulli (obtenue par Bienaymé-Chebychev) et celle de Hoeffding...
Pour Hoeffding, dans le cas d'une Bernoulli, on tombe sur l'inégalité , alors que l'inégalité que j'obtiens est , ce qui me parait trop beau pour être vrai...