
Find all
3 messages
- Page 1 sur 1
Changer simultanément les signes de  ne change rien au problème et permet de considérer
ne change rien au problème et permet de considérer  .
.
Changer le signe de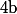 ne change rien non plus vu la symétrie de l'intervalle
ne change rien non plus vu la symétrie de l'intervalle  et permet de considérer
et permet de considérer 
Si=ax^2+bx+c\) sur
sur  alors
alors =2ax+b) et deux cas se présentent :
et deux cas se présentent :
 Soit
Soit 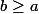 et
et  est croissante sur
est croissante sur  donc
donc
|\leq 1\Big)\ \Leftrightarrow\ <br />\Big(-1\leq f\big(-\frac{1}{2}\big)\text{ et } f\big(\frac{1}{2}\big)\leq 1\Big)\ \Leftrightarrow\ <br />-1+\frac{b}{2}-\frac{a}{4}+\leq c\leq 1-\frac{b}{2}-\frac{a}{4}\) où
où 
On a donc affaire à un polyèdre convexe dont on cherche le point le plus éloigné de l'origine.
C'est forcément un des sommets et on vérifie aisément que c'est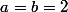 ,
,  qui donne
qui donne 
 Soit
Soit  ,
,  et
et  ) montre que le maximum est atteint pour
) montre que le maximum est atteint pour  ,
,  et donc
et donc  (ce qui est géométriquement parlant assez évident...)
(ce qui est géométriquement parlant assez évident...)
P.S. J'ai cherché un bon moment, mais je ne trouve pas de preuves "en claquant des doigts" alors que le résultat est extrêmement naturel...
Changer le signe de
Si
On a donc affaire à un polyèdre convexe dont on cherche le point le plus éloigné de l'origine.
C'est forcément un des sommets et on vérifie aisément que c'est
P.S. J'ai cherché un bon moment, mais je ne trouve pas de preuves "en claquant des doigts" alors que le résultat est extrêmement naturel...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En fait, j'ai un peu plus simple...
Toujours en posant=ax^2+bx+c\) , si on regarde les triplets
, si on regarde les triplets ) tels que
tels que ) ,
, ) et
et ) soient tout les trois dans
soient tout les trois dans  cela forme un parallélépipède (car les 3 vecteurs normaux forment une base de
cela forme un parallélépipède (car les 3 vecteurs normaux forment une base de  ) dont le point le plus éloigné de l'origine est évidement un des 8 sommets :
) dont le point le plus éloigné de l'origine est évidement un des 8 sommets :
1)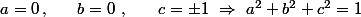
2)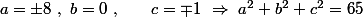
3)
Le point le plus éloigné est donc et on vérifie aisément que
et on vérifie aisément que =8x^2-1) vérifie bien les conditions demandées.
vérifie bien les conditions demandées.
Toujours en posant
1)
2)
3)
Le point le plus éloigné est donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
