Bonjour
Existe-t-il une preuve que l'algorithme de conversion de base trouve toujours les coefficients d_i de la représentation d'un nombre décimal n en base B tels que :
n = d_k * B^k + d_k−1 * B^(k−1) + ⋯ + d_1 * B^1 + d_0 * B^0
avec
n >= 0
b >= 2
B > d_i >= 0
J'ai cherché sur Google et je n'ai rien trouvé.
Je dois souligner que je sais intuitivement pourquoi cela fonctionne ; ce que je recherche, c'est une preuve mathématique solide.
L'algorithme de conversion de base convertit un nombre de base 10 vers une autre base B en le divisant successivement par B
Démonstration de l’algorithme de conversion en base B
6 messages
- Page 1 sur 1
Re: Démonstration de l’algorithme de conversion en base B
Bonjour,
Il suffit de voir que l'algorithme termine (un entier naturel décroît strictement jusqu'à valoir 0 en un nombre fini d'étapes) et qu'il y a un invariant de boucle qui garantit l'égalité entre l'entier de départ et le obtenu à la fin.
obtenu à la fin.
Il suffit de voir que l'algorithme termine (un entier naturel décroît strictement jusqu'à valoir 0 en un nombre fini d'étapes) et qu'il y a un invariant de boucle qui garantit l'égalité entre l'entier de départ et le
Re: Démonstration de l’algorithme de conversion en base B
GaBuZoMeu a écrit:Bonjour,
Il suffit de voir que l'algorithme termine (un entier naturel décroît strictement jusqu'à valoir 0 en un nombre fini d'étapes) et qu'il y a un invariant de boucle qui garantit l'égalité entre l'entier de départ et leobtenu à la fin.
Existe-il une preuve mathématique solide
Re: Démonstration de l’algorithme de conversion en base B
Ce que j'ai esquissé est une preuve mathématique solide. Je te laisse penser aux détails.
Re: Démonstration de l’algorithme de conversion en base B
GaBuZoMeu a écrit:Ce que j'ai esquissé est une preuve mathématique solide. Je te laisse penser aux détails.
C'est pas une preuve du tout, t'es sérieux là ?
Pour être plus précis :
dans la représentation d'un nombre décimal n en base B chaque coefficient d_i multiplie une puissance distincte de B
d_0 multiplie B^0, d_1 multiplie B^1, D_k multiplie B^k
Je veux une preuve que chaque reste peut être inséré dans la représentation de n en base B et que chacun des restes permet de multiplier des puissances distinctes de B, que chaque reste prend la place d'un d_i dans n en base B
r_0 doit correspondre à d_0 qui multiplie B^0
r_1 doit correspondre à d_1 qui multiplie B^1
r_k doit correspondre à d_k qui multiplie B^k
Il y a une preuve sérieuse de cela ?
Re: Démonstration de l’algorithme de conversion en base B
Je suis très sérieux. Et puisque tu as la flemme, je fais.
L'algorithme est le suivant
On prend en entrée l'entier naturel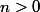 .
.
On initialise les variables locales ,
,  et
et  (la liste vide).
(la liste vide).
On boucle tant que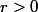 :
:

L'algorithme termine parce que la variable locale décroit strictement à chaque boucle. Elle finit forcément par valoir 0.
décroit strictement à chaque boucle. Elle finit forcément par valoir 0.
L'invariant de boucle est (je te laisse vérifier que c'est bien un invariant de boucle). À l'initialisation cet invariant de boucle est
(je te laisse vérifier que c'est bien un invariant de boucle). À l'initialisation cet invariant de boucle est  , donc il est aussi
, donc il est aussi  à la sortie, quand
à la sortie, quand 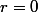 .
.
L'algorithme est le suivant
On prend en entrée l'entier naturel
On initialise les variables locales
On boucle tant que
- faire la division euclidienne de
ajouter
incrémenter
faire
L'algorithme termine parce que la variable locale
L'invariant de boucle est
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
