Continuité

[nada-top]

ni hao :happy3:

voilà un simple exo d'application mais vraiment ça me gène et je trouve que ça demande des outils qu'on a pas encore vu en cours pour le resoudre :

il s'agit d'étudier la continuité de la fonction :



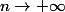
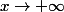
le probleme d'abord c'est le calcul de cette limite car j'ai et non :hum: ...bon j'ai pensé à utiliser l'exponentielle mais c'est sur c'est pas ce qui est demandé car on a pas encore vu mais bon voilà ce que j'ai pu faire avec ce que je viens de découvrir :
[TEX]3$g(x) = \left(\frac{x^n +x}{x^{2n+1 } + 1\right) \;\Leftrightarrow \; \left\{
\begin{array}{ll}
g(x) = \frac{e^{n ln(x)} + e^{ln(x)}}{e^{2n+1 ln(x)} + 1}\;\; \mbox{si}\;\; x>0\\
g(x) = \frac{e^{-n ln(x)} + e^{-ln(x)}}{e^{-(2n+1) ln(x)} + 1}\;\; \mbox{si}\;\; x0 je vois pas .:look_up: ça donne une forme indterminée à ce qu'il me parait.

ma question : comment peut-on calculer simplement ces limites rien qu'avec des outils élémentaires ? sinon ça m'interesse de voir la méthode générale ou qq indices pour le resoudre..

Merci

[Alexandre_de_Prepanet]

ok je vois où tu veux en venir

[Alexandre_de_Prepanet]

Je te conseille de ne pas utiliser l’exponentielle, tu peux t'en sortir mais c'est un peu délicat, surtout si tu ne l’as pas vu en cours.

Tu peux par contre étudier ta fonction f sur ] - ; -1] puis sur ]-1 ; 1[ puis sur [1 ; [

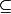
Si x ]-1 ; 1[ tu peux déterminer ta limite assez facilement
( ->0 qd n->)

Ensuite, est ce que tu sais calculer f(1) ? (essaye de vérifier que f(1) = 1)

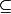
Pour x [1 ; [ factorise ton expression par au numérateur et au dénominateur, et tu verras des simplifications intervenir pour le calcul de ta limite.

[nox]

moi je dirai par x puissance n en haut et par x puissance 2n+1 en bas
comme toujours quand on a un quotient de polynomes et qu'on cherche une limite en l'infini -> terme de plus haut degré en facteur

[nox]

ca marche ca ?
ATTENTION c'est limite quand n tend vers l'infini et pas x !

[nada-top]

salut,

Tu peux par contre étudier ta fonction f sur ] - ; -1] puis sur ]-1 ; 1[ puis sur [1 ; [[/TEX]

tu voulais dire étudier f sur ]-\infty , -1[ et...(car la fonction n'est pas défini en -1 )

Ensuite, est ce que tu sais calculer f(1) ? (essaye de vérifier que f(1) = 1)

sure !! ...ben il suffit de rmeplacer on a bien f(1) = 1

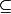
Si x ]-1 ; 1[ tu peux déterminer ta limite assez facilement
( ->0 qd n->)

donc si j'ai bien compris : si :
si :
et si : je dois étudier les cas selon la parité de n :
si n est paire alors :
et si n est impaire :
c ça ?...pour le calcul des limites je vais essayer mais déjà je vois pas de probleme . :we:
mais je serais curieuse de savoir comment faire avec l'exponentielle .

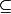
Ps : est le signe d'inclusion pour l'appartenance la commande latex c'est : \in

[nada-top]

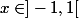
la limite si vaut 0 c'est ça ?

[Duche]

N'oublie pas que lim( ln( f(x,n) ) ) = ln( lim( f(x,n) ) ) :id:

[nada-top]

N'oublie pas que lim( ln( f(x,n) ) ) = ln( lim( f(x,n) ) )

je le connaissais pas pour l'oublier :lol5:
sinon comment ça peut m'aider ?

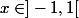
ps: qqn pour comfirmer la limite si car j'ai des doutes

[Alexandre_de_Prepanet]

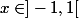
la limite si vaut 0 c'est ça ?

Non, si f(x) = x

[Mikou]

ca na riena faire dans le café mathematique.
Etudier la limite ou la continuité ??

[nox]

tu bosses jamais au café ? :we:

[nada-top]

Non, si

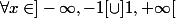
oui c'est logique merci :we: ...en fait mon 0 c'était pour ..ben j'ai factorisé par et ça me donne 0 , est-ce correct ?

[Alexandre_de_Prepanet]

Oui Nada, sur ces intervalles là, f est la fonction constante de valeur nulle.

[nada-top]

merci Alexandre :happy3: