Bonjour chères et chers matheux,
J'ai un problème à résoudre et j'ai besoin de votre aide.
J'ai les coordonnées cartésiennes d'un triangle et je cherche à trouver le centre du cercle circonscrit à ce triangle (cercle qui passe par les trois sommet du triangle)
Comment puis faire ?
Exemple :
Chaque sommet du triangle est determiné par ses coordonnées x, y
Donc je connais les coordonnées de chaque sommet du triangle :
x1,y1 ; x2,y2 ; x3,y3 et je cherche donc les coordonnées du centre du cercle qui seront x4,y4 en fonction des autres coordonnées.
J'espère avoir bien poser le problème et merci pour votre aide.
Bonne journée
Trouver le centre d'un cercle circonscrit
4 messages
- Page 1 sur 1
Les calculs ne sont pas difficiles mais un peu longs . Notons 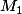 ,
, 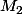 et
et 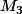 les sommets du triangle et
les sommets du triangle et  le centre du cercle circonscrit .
le centre du cercle circonscrit . 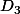 La médiatrice de
La médiatrice de 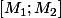 passe par le milieu
passe par le milieu ) de
de 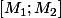 et a pour vecteur directeur
et a pour vecteur directeur ) normal à
normal à 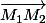 . On trouve ainsi facilement l'équation cartésienne de
. On trouve ainsi facilement l'équation cartésienne de 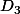 et de même celle de
et de même celle de 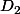 la médiatrice de
la médiatrice de 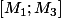 . Il n'y a plus qu'à résoudre le système linéaire de deux équations à deux inconnues formé par les équations de
. Il n'y a plus qu'à résoudre le système linéaire de deux équations à deux inconnues formé par les équations de 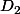 et
et 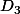 pour obtenir les coordonnées de O .
pour obtenir les coordonnées de O .
Imod
Imod
Merci à vous deux
Merci à vous deux pour votre aide.
J'ai trouver les équations que je cherchais ! :we:
J'ai trouver les équations que je cherchais ! :we:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 soit
soit 
 qui donne après développement et réduction un système linéaire en (x ; y)
qui donne après développement et réduction un système linéaire en (x ; y)