Le théorème de Bézout (pour les polynômes) s'énonce ainsi :
Deux polynômes A et B sont premiers entre eux si et seulement s'il existe dans K[X] deux polynômes Uo et Vo tels que :
AUo + BVo = 1
avec d°(Uo) < d°(B) et d°(Vo) < d°(A)
Comment expliquer cette dernière affirmation concernant les inégalités des degrés de polynômes ?
NB : J'appelle K[X] l'ensemble des polynômes.
Je vous remercie à l'avance pour vos salvatrices explications !
Théorème de Bézout pour les polynômes
3 messages
- Page 1 sur 1
Supposons que tu trouves 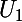 et
et 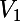 vérifiant :
vérifiant :
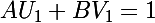
Alors, fais la division de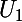 par B :
par B :
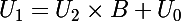 avec d°(
avec d°(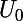 )<d°(B)
)<d°(B)
+BV_1=1)
=1)
Alors les polynômes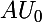 et
et ) sont nécessairement du même degré. Et comme :
sont nécessairement du même degré. Et comme :
d°(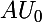 )=d°(
)=d°(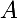 )+d°(
)+d°(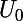 ) et que d°(
) et que d°() )=d°(
)=d°(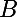 )+d°(
)+d°(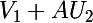 )
)
le fait que d°(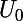 )<d°(
)<d°(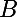 ) implique que :
) implique que :
d°(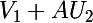 ) = d°(
) = d°(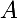 )+d°(
)+d°(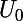 )- d°(
)- d°(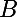 )<d°(
)<d°(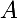 )+d°(
)+d°(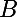 )- d°(
)- d°(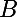 )=d°(
)=d°(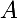 )
)
Ainsi, en posant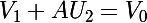 , on a bien :
, on a bien :
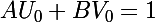
avec d°(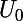 )<d°(
)<d°(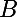 ) et d°(
) et d°(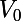 )<d°(
)<d°(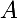 )
)
Par conséquent, si tu trouves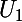 et
et 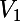 vérifiant :
vérifiant :
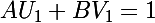
tu peux toujours en déduire deux autres polynômes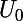 et
et 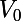 qui vérifieront :
qui vérifieront :
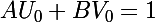
et qui vérifieront en plus la condition sur les degrés !
Alors, fais la division de
Alors les polynômes
d°(
le fait que d°(
d°(
Ainsi, en posant
avec d°(
Par conséquent, si tu trouves
tu peux toujours en déduire deux autres polynômes
et qui vérifieront en plus la condition sur les degrés !
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
