Méthode de jacobi et de Gauss Seidel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 23:38
-
 par kasmath » 12 Juin 2012, 14:22
par kasmath » 12 Juin 2012, 14:22
Bonjour ; je cherche le cours d'analyse numérique à fin de déterminée quand ses deux méthodes convergent
par Exp :

et la question se pose Sans calcule donner une condition suffisante sur

pour que les méthodes ditération de jacobi et de Gauss soit convergente .
et Merci davance
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 16:22
-
 par zork » 12 Juin 2012, 16:28
par zork » 12 Juin 2012, 16:28
il faut chercher le rayon spectral, s'il est inférieur à 1, la méthode converge
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 23:38
-
 par kasmath » 12 Juin 2012, 16:57
par kasmath » 12 Juin 2012, 16:57
La Relation Du Rayon Spectral ??
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 16:22
-
 par zork » 12 Juin 2012, 18:54
par zork » 12 Juin 2012, 18:54
je prend par exemple la méthode de jacobi: A=D-N avec D=I
donc D^(-1)N=N. N ayant des 0 sur la diagonale et des -bêta ailleurs
les valeurs propres de N sont:
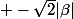
et 0
on note p le rayon spectral.
si

=0, la seule valeur propre de N serait 1 et la méthode de jacobi ne converge pas.
donc

est différent de 0 toujours
donc p(N)=
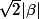
pour que p(N)<1, il faut que
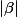
<

et la méthode converge
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 23:38
-
 par kasmath » 12 Juin 2012, 19:51
par kasmath » 12 Juin 2012, 19:51
SOYANT UN PEUT CONCRET ,
D'APRES SE QUE TU A ECRIT

cela donne
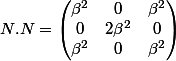
je voie QUE LE MAX EST
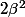
D'OU SA VIENT LA RACINE
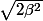
Merci BCP
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 16:22
-
 par zork » 12 Juin 2012, 20:01
par zork » 12 Juin 2012, 20:01
dans la matrice N, ce sont des -bêta, puis tu cherches les valeurs propres de N
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités