Hyperplan dense et théoreme des résidus
23 messages
- Page 1 sur 2 - 1, 2
Hyperplan dense et théoreme des résidus
On sait qu'il est possible de trouver des hyperplans denses dans un evn (souvent appelés édredon ou nuage :) ) par exemple : H = { P apartenant a R[X] tel que P(1) = 0 }
Est t il possible de former un hyperplan dense grace o Théoreme des résidus qui stipule en gros que si l'intégrale de moins l'infini a plus l'infini d'une fraction rationnelle (complexe) existe alors la somme des coefficients de ces poles est nulle...
Par ailleurs connaissez vous d'autre types d'hyperplan dense
Merci chers amis des maths
Est t il possible de former un hyperplan dense grace o Théoreme des résidus qui stipule en gros que si l'intégrale de moins l'infini a plus l'infini d'une fraction rationnelle (complexe) existe alors la somme des coefficients de ces poles est nulle...
Par ailleurs connaissez vous d'autre types d'hyperplan dense
Merci chers amis des maths
Ce genre de question a été posé une fois dans un autre forum : lien
en espérant que cela puisse t'aider un peu...
en espérant que cela puisse t'aider un peu...
yos a écrit:Bonsoir.
Je propose E l'ev des suites réelles convergentes muni de la norme infinie et H le sev des suites de limite nulle.
Bonjour,
Je n'en suis pas si sur...j'ai comme l'impression que H n'est pas dense en tout cas pas pas avec la norme infinie...car si
Il faut réussir à trouver un hyperplan qui n'est pas fermé (puisqu'il doit être dense...) et donc nécessairement se placer en dimension infinie (comme l'a fait Yos dans son exemple) mais la forme linéaire dont est issue l'hyperplan ne doit pas être continue, ce qui n'est pas le cas dans l'exemple ci dessus puisqu'avec une suite de suite qui converge vers la suite nulle :
En attendant je n'ai, pour l'instant, rien de mieux à proposer... :euh:
C'est pas très dur. Je vais essayer de me remémorer le truc (entre deux copies à corriger). Il est clair que le sens non évident est :
" f pas continue entraîne H dense ".
Le premier point auquel on pense pas forcément est que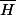 est aussi un sev. Du coup il n'y a que deux possibilités (pour des raisons de (co)dimension) :
est aussi un sev. Du coup il n'y a que deux possibilités (pour des raisons de (co)dimension) :
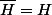 auquel cas H est fermé.
auquel cas H est fermé.
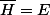 auquel cas H est dense.
auquel cas H est dense.
Donc tu peux partir de H fermé et prouver que f est continue. Ca doit se faire à l'aide des caractérisations des applications linéaires continues (genre "borné sur une boule").
Je dirais que c'est vrai dans un evt et pas seulement un evn (?)
Si tu parviens à compléter la preuve, écris-là!
" f pas continue entraîne H dense ".
Le premier point auquel on pense pas forcément est que
Donc tu peux partir de H fermé et prouver que f est continue. Ca doit se faire à l'aide des caractérisations des applications linéaires continues (genre "borné sur une boule").
Je dirais que c'est vrai dans un evt et pas seulement un evn (?)
Si tu parviens à compléter la preuve, écris-là!
Bonsoir,
alors voilà ce que j'ai fait grâce aux conseils de Yos, dites moi ce que vous en pensez...
=H) est un hyperplan et
est un hyperplan et 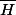 est un espace vectoriel aussi (pas dur). Puisque
est un espace vectoriel aussi (pas dur). Puisque  est de codimension 1 (il existe
est de codimension 1 (il existe 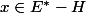 tq.
tq. \bigoplus H) ) et que
) et que 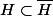 , on a que deux possibilités : soit
, on a que deux possibilités : soit 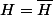 et
et  est fermé soit
est fermé soit 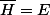 .
.
Le but est de montrer qu'il y a équivalence entre non continue et
non continue et ) dense dans
dense dans  . Comme il n'y a que deux possibilités, cela revient à montrer que si H est fermé alors f est continue :
. Comme il n'y a que deux possibilités, cela revient à montrer que si H est fermé alors f est continue :
Nous supposons donc H fermé et nous allons montrer que f est continue avec la caractérisation : f est bornée sur une boule.
\bigoplus H) avec
avec 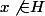 , on pose
, on pose 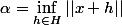 .
.
Si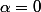 alors il existe une suite
alors il existe une suite 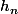 d'éléments de H tq
d'éléments de H tq 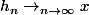 ce qui est impossible car H est fermé et
ce qui est impossible car H est fermé et 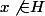 donc
donc 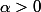 .
.
Pour tout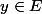 il existe
il existe 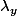 dans le corps de base et
dans le corps de base et 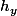 dans H tq
dans H tq 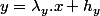 , si
, si ) alors
alors 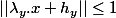 donc
donc 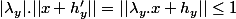 (avec
(avec 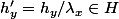 ) et donc :
) et donc :  d'ou une majoration de
d'ou une majoration de 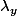 par
par 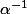 sur la boule unité.
sur la boule unité.
Donc pour tout) ,
, |=|f(\lambda_y.x+h_y)|=|\lambda_y|.|f(x)|\leq\alpha^{-1}|f(x)|)
 étant fixé,
étant fixé,  est bien bornée sur la boule unité et donc continue ssi
est bien bornée sur la boule unité et donc continue ssi ) est fermé, et avecc ce qui à été dit avant on a : f non continue ssi
est fermé, et avecc ce qui à été dit avant on a : f non continue ssi ) dense.
dense.
Reste à savoir si cela est vrai dans espace topologique (non normé), je n'en ai aucune idée (si quelqu'un a une idée...) mais dans ce cas on ne peut plus passer par la continuité de f autrement qu'avec "l'image réciproque d'un ouvert est un ouvert", l'argument "bornée" n'ayant plus de sens...
alors voilà ce que j'ai fait grâce aux conseils de Yos, dites moi ce que vous en pensez...
Le but est de montrer qu'il y a équivalence entre
Nous supposons donc H fermé et nous allons montrer que f est continue avec la caractérisation : f est bornée sur une boule.
Si
Pour tout
Donc pour tout
Reste à savoir si cela est vrai dans espace topologique (non normé), je n'en ai aucune idée (si quelqu'un a une idée...) mais dans ce cas on ne peut plus passer par la continuité de f autrement qu'avec "l'image réciproque d'un ouvert est un ouvert", l'argument "bornée" n'ayant plus de sens...
Bonjour,
je ne comprends pas pourquoi "etre bornée" n'a plus de sens ? Ce qui compte, c'est que l'espace d'arrivée, le corps des scalaires, soit métrique, non ? Pour moi, f non bornée signifie
des scalaires, soit métrique, non ? Pour moi, f non bornée signifie
||_{\mathbb{K}}>A) .
.
J'y arriverais si je savais montrer que la suite des\over f(x_n)}x_n) tend vers a, où les
tend vers a, où les  sont dans un ouvert sur lequel f n'est pas bornée.
sont dans un ouvert sur lequel f n'est pas bornée.
Une petite précision s'il vous plaît : dire que la suite) tend vers a, c'est bien dire que tout ouvert U de E contenant a contient tous les
tend vers a, c'est bien dire que tout ouvert U de E contenant a contient tous les  pour n assez grand ?
pour n assez grand ?
tize a écrit:Reste à savoir si cela est vrai dans espace topologique (non normé), je n'en ai aucune idée (si quelqu'un a une idée...) mais dans ce cas on ne peut plus passer par la continuité de f autrement qu'avec "l'image réciproque d'un ouvert est un ouvert", l'argument "bornée" n'ayant plus de sens...
je ne comprends pas pourquoi "etre bornée" n'a plus de sens ? Ce qui compte, c'est que l'espace d'arrivée, le corps
J'y arriverais si je savais montrer que la suite des
Une petite précision s'il vous plaît : dire que la suite
Zebulon a écrit:Bonjour,
je ne comprends pas pourquoi "etre bornée" n'a plus de sens ? Ce qui compte, c'est que l'espace d'arrivée, le corpsdes scalaires, soit métrique, non ? Pour moi, f non bornée signifie
.
J'y arriverais si je savais montrer que la suite destend vers a, où les
sont dans un ouvert sur lequel f n'est pas bornée.
Une petite précision s'il vous plaît : dire que la suitetend vers a, c'est bien dire que tout ouvert U de E contenant a contient tous les
pour n assez grand ?
La difficulté (pour moi) vient du fait que la définition d'une application lineaire continue sur un evn fait appel justement à la norme de cette evn : l'image de la boule unité (bornée) est bornée. Mais dans un espace topologique pur (sans norme) la définition n'a plus de sens puisque qu'il n'y a pas de boule unité (la boule unité etant définie par une norme...). J'en suis réduit à devoir utiliser la définition topologique de la continuité (l'image réciproque d'un ouvert est un ouvert).
Pour ta question, la réponse est oui :
Encore moi, juste pour dire que ma démonstration n'est pas très élégante...j'ai trouvé ceci sur le net :
Supposons f non continue ,elle n'est donc pas continue en 0 et il existe tq
tq 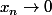 et
et \not{\to}0) , il existe donc
, il existe donc  croissante tq
croissante tq }\)|>\varepsilon) . En posant
. En posant }}{f\(x_{\varphi(n)}\)}) , on a
, on a 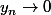 et
et =1) pour tout n. Maintenant, f n'etant pas nulle, on prend
pour tout n. Maintenant, f n'etant pas nulle, on prend 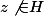 et on pose
et on pose ) .
. 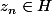 pour tout entier n et
pour tout entier n et 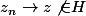 , H n'est donc pas fermé.
, H n'est donc pas fermé.
On doit pouvoir transposer cette preuve avec des ouverts dans le cas d'un espace topologique mais j'ai la flemme d'essayer maintenant, je laisse Zébulon tenter le coup.
Sinon pour un espace vectoriel topologique j'ai trouver ceci mais il n'y a pas de démonstration...
Supposons f non continue ,elle n'est donc pas continue en 0 et il existe
On doit pouvoir transposer cette preuve avec des ouverts dans le cas d'un espace topologique mais j'ai la flemme d'essayer maintenant, je laisse Zébulon tenter le coup.
Sinon pour un espace vectoriel topologique j'ai trouver ceci mais il n'y a pas de démonstration...
tize a écrit: pourquoiest fermé ?
Si
C'est comme dans R^3, les plans affines associés à une fl forment un feuilletage parallèle de l'espace.
Pour la preuve précédente, j'ai utilisé une indication du cours de topologie de Choquet (dieu ait son âme). Mais c'était assez pauvre comme indication et j'ai pas trouvé tout de suite. Ta preuve est très bien aussi, et il est possible que dans une certaine mesure, ce soit la même chose. Je regarderai ce qu'il en est dans un evt.
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
