Définition de la norme L2

[tlemcenvisit]

Salut
J'ai besoin de la définition de la norme L2
Merci de bien vouloir m'aider

[kgb]

en général, pour une matrice A=a(j,k) elle est définie comme la racine carrée de la somme sur j et k des carrés de a(j,k), si tu préfères :
sqrt(somme sur j,k (a(j,k)))

[quinto]

Salut
J'ai besoin de la définition de la norme L2
Merci de bien vouloir m'aider

Bein ca dépend un peu de là où tu te places.
D'une manière générale c'est l'intégrale du carré de la valeur absolue de ton objet.

[mathématrique]

alors en règle générale la norme L2 c'est quand tu n'es pas assez en L1....sauf si t'as des problèmes financiers...

[mathox]

D'une manière générale c'est l'intégrale du carré de la valeur absolue de ton objet.
j'ai mal à la tête quinto

[khivapia]

en fait c'est la norme issue du produit scalaire sur l'espace considéré, en général.

Par exemple pour les fonctions de carré intégrable le produit scalaire de f par g est

[Ian]

en fait c'est la norme issue du produit scalaire sur l'espace considéré, en général.

Par exemple pour les fonctions de carré intégrable le produit scalaire de f par g est

Bien que la question soit assez vague ("definition de la norme L2"), je rejoindrai plutot Quinto que Khivapia sur la reponse. Il me semble qu'on ne peut pas forcement supposer l'existence d'un produit scalaire sur un espace norme muni de la norme L2. Ceci dit, comme aucun contre exemple ne me vient a l'esprit pour le moment, a part peut-etre l'espace des fonctions quasi-periodiques sur un interval compact (c'est un souvenir plutot lointain et donc pas forcement rigoureux), si qqun me prouve le contraire, je suis preneur. :rolleyes:

A+

[thomasg]

Bonjour

voici ce que donne W. RUDIN dans "analyse réelle et complexe" page 62:

Définition 1 : pour toute fonction mesurable à valeurs complexes définie sur un espace mesuré X, on pose:

norme L2(f)=[int sur X(|f|^2)]^(1/2)

Définition 2 : on appelle espace L2 l'ensemble des fonctions pour lesquelles la norme L2 est finie.

Si il y a des questions sur ces définition je peux y répondre.

Au revoir

[Ian]

Bien vu. Cette definition recouvre la norme l2 pour les suites, la norme 2 (ou Euclidienne) pour les espaces R^n, la norme L2 pour les espaces de fonctions etc..., en function de la mesure que l'on a sur X.

Pour reprendre ma question de tout a l'heure: est-il possible de trouver un espace norme muni de la norme L2 ou cette norme L2 ne peut provenir d'un produit scalaire? A priori je dirai que oui, mais un exemple relativement simple serait le bienvenu...

A+

[khivapia]

Bien que la question soit assez vague ("definition de la norme L2"), je rejoindrai plutot Quinto que Khivapia sur la reponse. Il me semble qu'on ne peut pas forcement supposer l'existence d'un produit scalaire sur un espace norme muni de la norme L2. Ceci dit, comme aucun contre exemple ne me vient a l'esprit pour le moment, a part peut-etre l'espace des fonctions quasi-periodiques sur un interval compact (c'est un souvenir plutot lointain et donc pas forcement rigoureux), si qqun me prouve le contraire, je suis preneur. :rolleyes:

A+

oui en effet j'avais confondu la norme L2 et la norme 2 en général.

[quinto]

"Cette definition recouvre la norme l2 pour les suites, la norme 2 (ou Euclidienne) pour les espaces R^n, la norme L2 pour les espaces de fonctions etc..."

C'est pour celà que je parlais d'intégrale, car ca permettait de considérer toutes les mesures (comptage lebesgue etc) en une seule définition.;)
Je rejoindrai donc la définition du Rudin.
A+

[khivapia]

Bonjour à tous

je suis tout à fait d'accord avec ce qui a été dit

alors avec cette définition (norme de f = racine de l'intégrale du module carré de f) la norme L2 est toujours la norme associée au produit scalaire (f,g) = intégrale de (conjugué de f)*g

En effet elle vérifie l'égalité de la médiane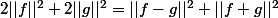 (propriétés du module dans C et linéarité de l'intégrale ).


Ce n'est en revanche pas le cas avec les normes p pour p différent de 2



PS : merci thomasg pour le numéro de la page dans le Rudin

[Anonyme]

Dans l'espace des fonctions de carré intégrable définies sur un intervalle [a;b], la norme L2 d'une fonction f est la racine carrée de l'intégrale entre a et b du carré de f.

[thomasg]

c'est un cas particulier de celle que j'ai donnée.