3=0

Bon, j'ai regarder si cette petite "énigme" avait déjà été posée mais la fonction recherche me met "aucun résultat" quoi que je mette (même des mots qui sont de partout (?))

Je le dis tout de suite c'est niveau lycée alors laissez les chercher...

Soit x un réel tel que x²+x+1=0
alors on a x+1=-x²
mais aussi x(x+1)+1=0 en remplaçant on obtient x(-x²)+1=0 c'est à dire
et donc x=1 et 1+1+1=0
:hein:

Bonjour

Il me semblait bien l'avoir déjà rencontrée :
Recherche avancée
Mots-clef : reel complexe
Recherche dans le forum Enigmes
Topic "Impossible"

a oui désolé déjà posté

En fait ton truc est faux dès le début car il n'existe pas de x réel tel x^2+x+1=0 donc tout le reste est faux ;) désolé ce n'est pas pour today que 3=0 ;)

Taupin a écrit:En fait ton truc est faux dès le début car il n'existe pas de x réel tel x^2+x+1=0 donc tout le reste est faux désolé ce n'est pas pour today que 3=0

Tu es au lycée Taupin?????

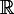
les solutions x²+x+1=0 n'appartiennent pas à car le delta est Négative !!

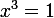
les solutions de cette equation qui appartiennent à sont : qui sont aussi les solutions de dans

on n'a pas le droit de répondre ! :cry:

Taupin a écrit:on n'a pas le droit de répondre !

Qui n'a pas le droit de répondre?

Taupin a écrit:on n'a pas le droit de répondre !

Je cite gol_di_grosso, l'auteur du problème : "Je le dis tout de suite c'est niveau lycée alors laissez les chercher...". C'est pour cela que je te demande si tu es au lycée...

Pas si évident pour des lycéens de bien comprendre où est le bug. D'ailleurs ce n'est pas évident non plus pour certains de mes collègues de spé qui ont eu du mal à donner le bon argument

Citation:Posté par Taupin
En fait ton truc est faux dès le début car il n'existe pas de x réel tel x^2+x+1=0 donc tout le reste est faux désolé ce n'est pas pour today que 3=0

Voila un raisonnement qui montre que la subtilité n'est pas forcement comprise :we: (comme raito d'ailleurs!)

En fait il n'y a aucune erreur dans le raisonnement, c'est juste la conclusion (3=0) qui est fausse.

Salut à tous :happy3:

Cet énoncé illustre bien l'utilisation abusive et injustifiée des <=> par les lycées :lol3:

En effet pas évident pour des lycéens.
Voila le meme probleme simplifié ou la meme erreur de raisonnement est faite mais est plus flagrante selon moi (de plus il contredit l'argumentation de taupin et Raito) :

x=1 je multiplie par x j'obtiens x²=x or x=1 donc x²=1.
x=-1 est solution de x²=1 donc est solution de x=1 donc -1=1.

Oui ou simplement :

x=1 d'où en multipliant par x : x²=x.
0 est solution donc en remplaçant dans la première égalité 0=1.

Nightmare a écrit:Oui ou simplement :

x=1 d'où en multipliant par x : x²=x.
0 est solution donc en remplaçant dans la première égalité 0=1.

Ah ouais encore plus simple

Taupin a écrit:on n'a pas le droit de répondre !

J'ai penser que ça pouvais déstabiliser les lycéens plus que les autres qui sont habitués ou qui voient tout de suite l'arnaque :happy2:

je me souviens,ma prof de terminale nous avait montré ce truc au premier cours,pour nous faire comprende qu il étais important d utiliser(et de distinguer) "implique" et "equivaut a"

Nightmare a écrit:Oui ou simplement :

x=1 d'où en multipliant par x : x²=x.
0 est solution donc en remplaçant dans la première égalité 0=1.

Il n'y a pas de vraie confusion si le lycéen est bien connaisseur des propriétés algébriques dans IR.

Si a=b alors pour tout c non inversible (sous entendu non nul) , c x a = c x b.

En particulier, pour c=a, a²=ab, a étant non nul sous ces conditions.

Et c'est là que la conclusion s'avère contradictoire, comme l'avait déjà dit bitonio.

Hyp a écrit:Si a=b alors pour tout c non inversible (sous entendu non nul) , c x a = c x b.

C'est vrai pour tout c inversible ou non .

Hyp a écrit:En particulier, pour c=a, a²=ab, a étant non nul sous ces conditions.

C'est vrai même si a est nul . mais bien sûr les réciproques sont fausses .

Comme quoi , implication et équivalence n'est pas si simple !

Imod

Nightmare a écrit:Oui ou simplement :

x=1 d'où en multipliant par x : x²=x.
0 est solution donc en remplaçant dans la première égalité 0=1.

Mouais !!

J'aime cet exemple!!

Patastronch a écrit:x=1 je multiplie par x j'obtiens x²=x or x=1 donc x²=1.
x=-1 est solution de x²=1 donc est solution de x=1 donc -1=1.

Celui là aussi !!

Alala vous voulez absolument mettre en défaut le monde des maths ? :cry: