Pti probleme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 07 Déc 2007, 10:48
par smooth5185 » 07 Déc 2007, 10:48
Oui bonjour,
Voila j'au une inegalité a prouver qui pourra m'etre tres utile pour le suite d'un probleme:
montrer que pour tout k appartenant a R:
1+(k+k')^2 Merci de votre aide.
-
blackpearl
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Nov 2007, 13:45
-
 par blackpearl » 07 Déc 2007, 10:57
par blackpearl » 07 Déc 2007, 10:57
1²+(k+k)²;)2(1+k²)(1+k²)
essayes de développer sa, normalement sa devrai marché
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 07 Déc 2007, 11:07
par smooth5185 » 07 Déc 2007, 11:07
j'obtiens: 1+(k+k')^2=1-2k^2*k'^2-2kk'
mais apres je vois pas
-
blackpearl
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Nov 2007, 13:45
-
 par blackpearl » 07 Déc 2007, 12:11
par blackpearl » 07 Déc 2007, 12:11
voila ou j'en ss moi;
bon , (1+k+k')(1-k-k');)-2(1+k²+k²+k²k²)
1-k²-2kk-k²;)-2(1+k²+k²+k²k²)
essaye de ramener d'un seul coté et tu simplifies jusk ou sa se vois que c inférieure, je vais le faire moi aussi et je te rendrai la réponse plus tard.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 07 Déc 2007, 12:14
par xyz1975 » 07 Déc 2007, 12:14
Bonjour,
Considérez la différence puis montrez que cette différence est positive (ou négative):
2(1+k²)(1+k'²)-1-(k+k')² =1+k²+k'²+2(kk')²-2kk'=1+(k+k')²+2(kk')².
Cette dérnière est positive alors la première l'est aussi d'où le résultat souhaité.
-
blackpearl
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Nov 2007, 13:45
-
 par blackpearl » 07 Déc 2007, 12:25
par blackpearl » 07 Déc 2007, 12:25
-2(1+k²+k²+k²k²) je vois pas comment sa sa pourrai être positif!!!
-
blackpearl
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Nov 2007, 13:45
-
 par blackpearl » 07 Déc 2007, 12:37
par blackpearl » 07 Déc 2007, 12:37
c bon c vrai, c positif :id:, mais je pense pas que c sa la question! elle veut avoir une relation entre k et k'
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 07 Déc 2007, 13:28
par smooth5185 » 07 Déc 2007, 13:28
non c'est bon
xyz1975 a raison en faisant la diff on y arrive
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 17:39
par franz2b » 07 Déc 2007, 17:39
(1 + k'^2) - [1 + (k + k')^2] = 2 + 2k'^2 + 2k^2 + (kk')^2 - 1 - k^2 - k'^2 - 2kk')
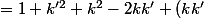^2)
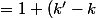^2 + (kk')^2 > 0)
Vive Fourier (hein seb

)
Et tout ca en LaTeX s'teuplait!
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 07 Déc 2007, 20:10
par xyz1975 » 07 Déc 2007, 20:10
franz2b a écrit:(1 + k'^2) - [1 + (k + k')^2] = 2 + 2k'^2 + 2k^2 + (kk')^2 - 1 - k^2 - k'^2 - 2kk')
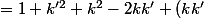^2)
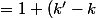^2 + (kk')^2 > 0)
Vive Fourier (hein seb

)
Et tout ca en LaTeX s'teuplait!
Sauf qu'un2 oublié mais c'est pas grave....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités