Pb de notaions

Pour les notations des dérivées "à la physicienne" on utilise svt dA(t)/dt ou "d ronde" à la place de d.
Quelle difference.Qd utiliser l'une? l'autre?
Merci

On utilise les d droits pour les fonctions d'une variable et les d ronds pour les fonctions de plusieurs variables.
Galt

La distinction est importante car on peut donner un sens mathématique à 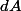ou 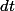(ce sont des différentielles), indépendamment de celui de la fonction dérivée de qui s'écrit , avec un vrai quotient.
En revanche, la notation pour les dérivées partielles, où est une fonction de plusieurs variables, et purement symbolique ; pris isolémen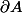t, et ne veulent rien dire.

Maintenant, les physiciens ont l'habitude de ne pas expliciter les variables dont dépendent leurs fonctions, en écrivant par exemple au lieu de ou , ce qui peut prêter à confusion. (De plus, ils ont tendance à utiliser la notation 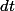pour désigner non pas une différentielle mais un "accroissement infiniment petit de la variable ", ce qui a priori ne signifie pas grand chose de rigoureux).

Qu'est ce qu'1 différentielle?

En quel niveau es-tu ?

Les différentielles se voient en 1ére année post-bac


Jord

La différentielle de f en a c'est l'application notée définie par :
(t dans R)

En notant abusivement x l'application identité sur R, l'application qui est alors la différentielle de x ne dépend pas de a et on la note simplement dx qui est définie par :
(t dans R)

Pour tout t de R :
.
Soit encore :

On omet parfois le a de et on remplace abusivement a par x dans f'(a) pour obtenir l'écriture raccourcie et on retrouve la relation : .


jord

Non inscrit a écrit:Qu'est ce qu'1 différentielle?

Limitons-nous au cas d'une fonction d'une variable , qu'on va supposer dérivable en un certain réel . Notons traditionnellement le nombre dérivé de en . On appelle différentielle de en l'application linéaire de dans définie par :
.
On note cette application .

Maintenant, dans le cas particulier de la fonction , en tout point , sa dérivée vaut , et sa différentielle en n'est autre que l'identité :
.
On fait alors l'abus de notation qui consiste à confondre et la fonction (je sais, c'est mal), et on note (on omet aussi le , puisque cette application ne dépend pas de en vérité).
En reprenant la fonction de tout-à-l'heure, on voit que sa différentielle en peut s'écrire :
.
D'où la fameuse notation :
.

Bien sûr, cela a l'air extrêmement lourd pour pas grand chose. En fait, la notion de différentielle se justifie pleinement lorsqu'on veut travailler avec des fonctions de plusieurs variables (voire une infinité de variables !). En effet, la définition de la différentielle en tant qu'application linéaire se prolonge dans cette situation, et on peut généraliser toute la théorie des fonctions dérivables d'une variable aux fonctions de plusieurs variables de cette façon. En revanche, la notion de dérivée partielle ne suffit pas pour généraliser toute cette théorie.

Edit : mon post fait double emploi avec le précédent, que je n'ai pas vu pendant que j'écrivais... (Mais Nightmare mélange les et les ).

Merci bcp phenomene.
1 petit detail: Quelle difference entre differentielle exacte et forme différentielle (differentielle qui n'est pas exacte)?

Je vais dire des choses simplifiées à l'extrême
Si f est une fonction de R dans R , on appelle différentielle de f l'expression (il faudrait probablement des d ronds, mais je n'en suis pas certain et je ne sais pas les faire). C'est une différentielle exacte.
Une expression de la forme n'est pas toujours la diférentielle d'une fonction, parce que, pour une fonction de 2 variables, on a (c'est pareil de dériver d'abord par rapport à x, puis par rapport à y, ou dans l'autre sens. Ainsi, dans l'expression , pour qu'elle soit la différentielle d'une fonction, il faut que (en fait, c'est même une condition nécessaire et suffisante, si je me souviens bien)
Ainsi par exemple n'est pas une différentielle exacte.
Voila en gros le principe

Bonsoir, Galt a dit l'essentiel, mais comme il ne sait pas faire les 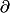(le code 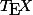est tout simplement \partial, Galt) et que c'est important, je vais reprendre un peu tout ça, en essayant d'expliquer les choses intuitivement, à la physicienne comme on dit (aucune rigueur n'est assurée !).

Considérons une fonction de deux variables (pour simplifier) qu'on note et . La différentielle de est donnée par :
,
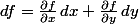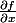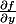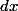où et désignent les dérivées partielles de par rapport à la première et la deuxième variables respectivement, et et 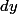sont les différentielles des fonctions de base et respectivement.
Bon, si l'on ne sait pas ce qu'est une différentielle mais qu'on veut pouvoir faire de la physique avant d'avoir eu un cours sur le sujet, on peut essayer de voir ça intuitivement. Pour un physicien,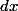 désigne un accroissement infiniment petit de l'abscisse , et 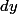un accroissement infiniment petit de l'ordonnée . Lorsque et varient ainsi de façon infinitésimale, varie en conséquence de façon infinitésimale, cette variation est 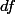. Elle est obtenue en ajoutant la variation de par rapport à (c'est-à-dire la dérivée partielle 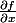) multipliée par la variation de (c'est-à-dire 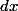) et la quantité analogue par rapport à la variable .
Bien entendu, ces notions d'"infiniment petit" ne veulent pas dire grand chose, rassurons-nous en disant que les différentielles ont un vrai sens mathématique qui rend tout ça rigoureux.

Maintenant, étant données deux fonctions et des deux variables et , la quantité suivante a un sens rigoureux également :
.
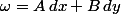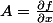On dit que est une forme différentielle. On dit que c'est une différentielle exacte s'il existe une fonction telle que et 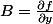, ce qui nous ramène à la situation précédente :
.
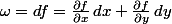Mais il n'y a a priori aucune raison pour que ce soit le cas. On peut vérifier (je suppose sans le dire que les fonctions mises en jeu admettent autant de dérivées partielles qu'on veut) qu'une condition nécessaire et suffisante pour que soit une différentielle exacte est :
.
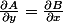Cela revient à dire qu'on a :
,
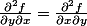et c'est le fameux théorème de Schwarz, qui affirme que l'ordre dans lequel on effectue des dérivations partielles successives n'a pas d'importance (à condition que les fonctions soient suffisamment régulières, encore une fois on le suppose ici).

Des formes différentielles apparaissent naturellement en physique, et je vais me risquer à essayer de donner un exemple montrant la différence avec des différentielles exactes au niveau physique ; n'étant pas physicien, j'espère ne pas dire trop de bêtises.
Lors du déplacement d'une masse ponctuelle (pour simplifier), les physiciens définissent le travail d'une force, noté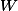 . C'est une énergie. Si l'on considère un déplacement "infiniment petit", on aura un "travail élémentaire" que les physiciens notent . Attention, la notation est dangereuse, car ce n'est a priori qu'une forme différentielle. Le ressemble à s'y méprendre à un , mais ça doit être fait exprès pour semer la confusion dans le cerveau des étudiants. :lol5:
Les physiciens noteront :
.
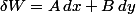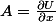Maintenant, il arrive que ceci soit une différentielle exacte. On dit dans ce cas que la force dérive d'un potentiel , et est précisément la fonction telle que et 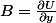. Il me semble (vérifiez auprès de votre physicien préféré) qu'on appelle énergie potentielle la quantité 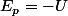. Bref, on dit que la force dérive d'une énergie potentielle, qui, au signe près, est notre fonction . Dans ce cas, on dit aussi que la force est conservative.
Mais il arrive que la force ne soit pas conservative. C'est le cas par exemple d'une force de frottement, qui est dissipative. Dans ce cas, la forme différentielle n'est pas exacte.

Pour saisir la différence, imaginons que notre masse décrive un mouvement pour revenir à son point de départ, par exemple un cercle . Quel est le travail total de la force considérée le long de ce parcours ? On le notera 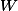, et c'est la somme de l'infinité de travaux infinitésimaux le long du parcours. Cette "somme" d'une infinité de quantités infiniment petites n'est autre qu'une intégrale le long du contour :
.
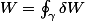On met un petit rond sur le signe intégral pour faire joli, et accessoirement pour dire qu'on intègre sur un contour fermé.
Bon, dans le cas où notre force dérive d'un potentiel, le travail total n'est autre que la variation de ce potentiel entre le point de départ et le point d'arrivée, qui sont confondus :
.
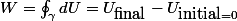Bref, le travail total de la force est nul, puisque le potentiel est le même au départ et à l'arrivée ( ne dépend que de et ). Ce résultat s'interprète en termes de conservation de l'énergie.
Maintenant, s'il y a des frottements, on se doute bien que l'énergie ne sera pas conservée, le travail total même sur une boucle fermée ne sera pas nul, et en effet, en l'absence de fonction potentiel , on ne peut pas écrire ce qui précède, et on aura en général :
.

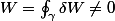Voilà, j'espère avoir donné une vision intuitive de ces choses difficiles. Si un mathématicien lit ces lignes, qu'il ait la gentillesse de ne pas me taper dessus pour mon manque de rigueur. Si un physicien passe par ici, qu'il rectifie mes éventuelles bêtises et qu'il n'hésite pas à me taper dessus. :marteau:

Amicalement.