Automorphisme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 12:23
par nada-top » 07 Sep 2006, 12:23
Bonjour,

est un automorphisme donc
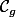
est symétrique par rapport à la première bissectrice .
résultat assez intuitif mais j'sais pas comment rédiger la preuve .
Merci :lol3:
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 12:26
par nox » 07 Sep 2006, 12:26
c'est intuitif ca ?
je vois pas d'où ca sort...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 12:31
par Flodelarab » 07 Sep 2006, 12:31
Ben oui.
As tu définis la symétrie en exprimant ça en fonction des coordonnées?
par la bijection tu dois retomber sur une démonstration cohérente
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 12:32
par nada-top » 07 Sep 2006, 12:32
g est bijective de E dans E donc C_g et C_g^{-1} sont symétriques par rapport à la première bissectrice , c'est pas intuitif ça ??
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 12:46
par nada-top » 07 Sep 2006, 12:46
oui j'ai tenté en commençant par :
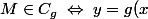 \;\Leftrightarrow\; x= g^{-1}(x) \; \Leftrightarrow \; M' \in C_{g^{-1}})
(avec
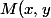)
et
)
sont symétrique par rapport à la première bissectrice)
et puisque
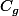
et

sont identiques alors .. :hein: mais je sens qu'il y a qq chose là qui ne vas pas :hum:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 12:49
par Flodelarab » 07 Sep 2006, 12:49
Plus j'y pense et plus je trouve que c faux.
ok. la courbe de l'automorphisme réciproque est le symétrique de Cg mais pas Cg symétrique de Cg ...
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 12:50
par nox » 07 Sep 2006, 12:50
ba oui c'est ce que je me disais...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 12:52
par nada-top » 07 Sep 2006, 12:52
mais g est bijective de E dans E :hein:(endomorphisme bijectif)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 12:56
par Flodelarab » 07 Sep 2006, 12:56
Et alors ?
Une permutation est bijective .... et pas involutive
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 12:59
par nox » 07 Sep 2006, 12:59
cf exponentiel...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 13:00
par Flodelarab » 07 Sep 2006, 13:00
nox a écrit:cf exponentiel...
c pas un automorphisme
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 13:10
par nada-top » 07 Sep 2006, 13:10
désolée j'ai pas encore vu la notion d'une application involutive mais d'aprés ce je trouve je suppose que tu voulais dire
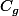
et

ne sont pas identiques , je vois pas pourquoi?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 13:16
par Flodelarab » 07 Sep 2006, 13:16
soit un ensemble E = {A,B,C} et g un automorphisme de E tel que:
g(A)=B
g(B)=C
g(C)=A
))
n'est pas égale a x
Ben oui mais on voudrait y=g(x) et x=g(y)
CQFD
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 13:18
par Flodelarab » 07 Sep 2006, 13:18
Au fait, si g(g(x))=x alors g est involutive
-
xon
- Membre Relatif
- Messages: 100
- Enregistré le: 24 Aoû 2006, 14:57
-
 par xon » 07 Sep 2006, 13:31
par xon » 07 Sep 2006, 13:31
que pensez vous de g(x)=2*x?
çà m'a tout l'air d'etre un automorphisme de (R,+) mais Cg n'est pas symetrique par rapport à la bissectrice
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 13:33
par Flodelarab » 07 Sep 2006, 13:33
xon a écrit:que pensez vous de g(x)=2*x?
çà m'a tout l'air d'etre un automorphisme de (R,+) mais Cg n'est pas symetrique par rapport à la bissectrice
meme principe
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 13:34
par nox » 07 Sep 2006, 13:34
wai mais plus simple :we:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 13:37
par nada-top » 07 Sep 2006, 13:37
oui je vois merci à vous , je crois que mon énoncé est faux :hum:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 14:15
par nada-top » 07 Sep 2006, 14:15
en voyant cet exemple je suis un peu perdue :
^3})

est une restriction de

sur
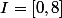
j'ai démontré que g est automorphisme , maintenant il est demandé de prouver que
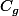
est symétrique par rapport à la première bissectrice , d'aprés le graphe ça sevoit bien ça :doh:

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités