La caverne de la taupe

Bonjours mes profs me conseillant de faire mes exercice avec d'autre je viens vous voir sur ce forum ^^ j'aurais donc beaucoup de questions de méthode pour mes TD et DM .

Donc voici pour mes premiers exos :

1)Soit Un tq U(n+1)=2Un + 1 et Uo=0
Determiner le terme générale de la suite Un .

Donc la je ne vois pas trop comment faire j'ai fait à la main les premières valeurs jusqu'à u4 et on trouve que la suite est ni arithmétique ni géométrique .

2) Soit Zn une suite complexe tq Zn+1=(1/3)(Zn+2Zn) ( Zn = complexe conjugué )
On veut montrer que Zn est convergente et donner sa limite .
Ici je ne vois pas par quoi commencer :/

Pourriez vous m'éclaircir sur la méthode à employer pour résoudre ses questions ?
Merci d'avance

Sishibo a écrit:Bonjours mes profs me conseillant de faire mes exercice avec d'autre je viens vous voir sur ce forum ^^ j'aurais donc beaucoup de questions de méthode pour mes TD et DM .

Donc voici pour mes premiers exos :

1)Soit Un tq U(n+1)=2Un + 1 et Uo=0
Determiner le terme générale de la suite Un .

Donc la je ne vois pas trop comment faire j'ai fait à la main les premières valeurs jusqu'à u4 et on trouve que la suite est ni arithmétique ni géométrique .

2) Soit Zn une suite complexe tq Zn+1=(1/3)(Zn+2Zn) ( Zn = complexe conjugué )
On veut montrer que Zn est convergente et donner sa limite .
Ici je ne vois pas par quoi commencer :/

Pourriez vous m'éclaircir sur la méthode à employer pour résoudre ses questions ?
Merci d'avance

salut
pour la 1, tu pourrais chercher s'il existe un nombre k tel que la suite telle = +k soit particulière

Salut pourrait tu expliquer ce que tu entend par particulière ?

En fait tu en as fait plein des comme ça au lycée. Sauf qu'on te guidait. En gros tu peux te débrouiller pour que Vn= Un+k soit géométrique (sauf erreur de ma part). Ensuite il faut faire l'aller retour entre les deux.

Ha oui je m'en rappelle maintenant je vais essayer merci .

Effectivement après calcul on a Un=2^n -1

Pour la question 2) vous auriez quelques pistes astucieuse svp ? ^^

Sishibo a écrit:Effectivement après calcul on a Un=2^n -1

Pour la question 2) vous auriez quelques pistes astucieuse svp ? ^^

suppose que Zn=15+12i
quel serait Zn+1 ?

Merci ;) Je viens de montrer que la suite était ou décroissante si Im(Zn)<0 ou croissante si Im(Zn)>0 je suppose qu'il faut que je trouve en minorant ... Comment faire en complexe ?

C'est bizarre quand même un complexe peu pas être plus grand ou plus petit qu'un autre ?

Sishibo a écrit:C'est bizarre quand même un complexe peu pas être plus grand ou plus petit qu'un autre ?

je poserais =+

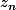
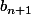
montre que est constant et exprime en fonction de puis en fonction de n

Montre que tend vers 0

Ha oui merci ;)