Congruences Spé Maths TS Modulo

[Tetdoss]

Salut à tous je suis en train de voir les congruences en Spé Math et j'ai un problème, enfin ce n'est pas vraiment un problème mais c'est plutôt une confusion que j'ai dans ma tête et qui me gène.

Quelques questions pour commencer :D .

Si on dit que 5 (4) veut dire 5 modulo 4 alors 5 modulo 4 = 1.
Mais alors on peut écrire :

5Pi = 3Pi (2Pi)
5Pi = Pi

Ce qui est absurde ! Il y a donc une différence entre 5 modulo 4 et 5 (4), j'aimerais bien la connaître :-° .

Alors j'ai pensé que le (4) s'applique des deux côtés de la parenthèses et non pas d'un seul côté mais veut toujours dire modulo 4 :

5Pi = 3Pi (2Pi)
Pi = Pi

C'est déjà plus logique.
Mais on peut aussi écrire 5Pi = 3Pi + 2kPi donc le module s'applique à droite du égal ou sur toute l'égalité ?

Ca m'embrouille toujours puisque si on prend l'exemple des congruences :

5 ;) 9 (4) = 5(4) ;) 9(4) = 1 ;) 1

C'est possible une relation de congruence sans modulo ??

De plus sur wikipédia il est dit que le signe = signifie "est égal à" et le signe ;) "identique à"... C'est quoi la différence entre ces 2 symboles ??


Je vais m'arrêter là car plus j'écris, plus je m'embrouille, merci d'avance :D .

[Pixis]

Alors oui, je vois que tu es pas mal embrouillé.
Il faut d'abord faire la différence entre "égal à" donc le signe est = et "modulo" dont le signe est ;), ce sont deux notions différentes.
le signe ne veut rien dire à lui tout seul : on dit qu'un nombre (a) est congru à un autre nombre (b) modulo un troisième (c), et ça s'écrit :

a;)b [c]

Mais concrètement, ça veut dire quoi ?
Pour comprendre ce que ça veut dire, la notion de diviseur est indispensable

:livre: Rappel : a est un diviseur de b est équivalent à : Il existe un entier relatif k tel que
b = k*a

Bon, du coup on comprend une définition de la congruence :

a;)b [c] veut dire que c est un diviseur de a-b

Par exemple : 17;)7 [5]
En effet, 17 - 7 = 10 et on a bien 5 qui est un diviseur de 10

Pour reprendre ton premier exemple :
tu as écrit :5Pi = 3Pi (2Pi)
Mais correctement on écrit :
5Pi 3Pi [2Pi] puisqu'en effet, 5Pi - 3Pi = 2Pi, et 2Pi est bien un diviseur de 2Pi

Mais il faut savoir qu'on peut parler de modulos d'une autre manière, comme tu l'as décrite :

[INDENT]" Si on dit que 5 (4) veut dire 5 modulo 4 alors 5 modulo 4 = 1. "[/INDENT]

5 modulo 4 est égal à 1 est équivalent à dire 5;)1 [4]
Encore une fois, on a bien 5-1 = 4 , et 4 est un diviseur de 4


:id: Pour info, je t'ai donné une définition de la congruence, mais il en existe plusieurs. Une autre très connue serait :
a b [c] équivalent à il existe k, entier relatif, tel que a = k*c + b
On remarque d'abord que si on soustrait b de chaque côté de l'égalité, alors on revient à la première définition
D'autre part, on remarque que ça ressemble fortement à la division euclidienne, la différence étant que, lorsqu'on est dans les congruence, le b n'est pas nécessairement positif et strictement inférieur à c.

J'espère t'avoir éclairci, bon courage !

[Tetdoss]

Merci beaucoup de ta réponse rapide Pixis !

Tu m'as effectivement pas mal éclairci, j'ai encore cependant quelques questions et confirmations à faire pour être sûr d'avoir bien compris...

Tu écris :
a ;) b [c]

le [c] s'applique à b c'est ça ? Ou à a ;) b ? Je suppose qu'il s'applique à b seulement,
et du coup on peut écrire b [c] = b + kc ?

mais du coup a = b + kc
mais si b [c] = b + kc, pourquoi on ne peut pas écrire a ;) b +kc ?
ça veut dire que b [c] n'est pas exactement égal à b + kc ?

D'après ce que j'ai compris il y a 2 types de modulo,

le modulo qui retourne le reste de la division euclidienne, exemple :
9 mod 4 = 1

et le modulo avec les crochets du style [n] qui veut dire + kn ?


Si ça peut être ça, c'est cool, au lieu d'écrire "le reste de la division de 9 par 4 = 1" j'écrirais sur mes copies "9 mod 4 = 1" et dans les autres cas comme la trigonométrie 5Pi [2Pi] ne peut pas être égal à Pi car [2Pi] = 2kPi mais par contre Pi est CONGRU à 5Pi [2Pi]

Ca à l'air de coller, je demande confirmation.

[Nightmare]

Bonjour,

attention, ceci :

:livre: Rappel : a est un diviseur de b est équivalent à : Il existe un entier relatif k tel que
b = k*a

Bon, du coup on comprend une définition de la congruence :

a;)b [c] veut dire que c est un diviseur de a-b

n'explique pas cela :

tu as écrit : 5Pi = 3Pi (2Pi)
Mais correctement on écrit :
5Pi 3Pi [2Pi] puisqu'en effet, 5Pi - 3Pi = 2Pi, et 2Pi est bien un diviseur de 2Pi

5pi et 3pi ne sont pas des entiers, on ne parle pas de "diviseurs" chez les réels. A la limite, on parlera de commensurabilité.

[Pixis]

Hum, ça à l'air de coller, mais non, tu n'as pas vraiment saisi le sens de mon explication.

le [c] s'applique à b c'est ça ? Ou à a b ? Je suppose qu'il s'applique à b seulement,
et du coup on peut écrire b [c] = b + kc ?

Non, le [c] ne "s'applique" pas à quoique ce soit. Au départ, tu as ton nombre a. Tu veux savoir à combien il est congru modulo un autre nombre c. Mais qu'est ce que ça veut dire ?
Si on devait le dire avec des termes non mathématiques, ça ressemblerait à ça :

Au départ tu as un nombre a, et tu veux savoir la différence entre ce a et un multiple quelconque de c

Prenons un exemple : Si tu as le nombre 18, tu veux savoir à combien il est congru modulo (modulo ici voudrait un peu dire "par rapport à") 4
C'est à dire, quelle est la différence entre 18 et un multiple de 4
Il existe une infinité de multiple de 4, par exemple 4, 8, 12, 40, 4000 etc ...
Donc la différence entre 18 et un multiple de 4 peut etre 14 puisque 18-1*4 = 14 mais aussi 2 puisque 18 - 4*4 = 18 - 16 = 2

Ce qui veut dire qu'on peut écrire :
1. 18 14 [4]
2. 18 2 [4]
mais encore
3. 18 6 [4] (puisque 18 - 3*4 = 6)

etc ...


Si tu as compris tout ça, on peut alors traduire ça avec des égalités :

1. 18 14 [4]
On a donc 18 - 1*4 = 14 donc 18 = 1*4 + 14

2. 18 2 [4]
On a donc 18 - 4*4 = 14 donc 18 = 4*4 + 14

3. 18 6 [4]
On a donc 18 - 3*4 = 14 donc 18 = 3*4 + 14

Donc en généralisant :
si a b [c] alors il existe un k dans tel que a = k*c + b

En somme, quand tu dis :

et le modulo avec les crochets du style [n] qui veut dire + kn ?

non, [n] ne veut pas dire + kn mais c'est un bon moyen mnémotechnique.

Je sais, c'est une notion pas très simple, et c'est encore plus dur à expliquer par écrit.

[Pixis]

5pi et 3pi ne sont pas des entiers, on ne parle pas de "diviseurs" chez les réels. A la limite, on parlera de commensurabilité.

Bien sûr, je n'ai pas réfléchi, merci pour la remarque !

[Tetdoss]

OK encore merci à vous deux, c'est compliqué cette histoire :hein:

je pense qu'il ne faut pas trop essayer de comprendre, même si comprendre aide à l'apprentissage

[HTML]Pour reprendre ton premier exemple :
tu as écrit :5Pi = 3Pi (2Pi)
Mais correctement on écrit :
5Pi 3Pi [2Pi] puisqu'en effet, 5Pi - 3Pi = 2Pi, et 2Pi est bien un diviseur de 2Pi[/HTML]

Quand je fais de la trigonométrie en tronc commun, on écrit 5Pi = 3Pi [2Pi]. Pourquoi ? Pour simplifier les choses je pense ?

Ce que je comprends maintenant c'est que ce [n] s'utilise uniquement dans des relations de congruence. Et qu'il ne faut pas confondre le modulo de maths [n] avec le modulo a mod b qui renvoie un résultat comme en informatique.

J'ai trouvé une discussion intéressante que je vais lire de suite :

http://sciences.siteduzero.com/forum-83-607378-p1-le-modulo.html

Effectivement, c'est très dur de s'expliquer à l'écrit...

[Tetdoss]

Bon j'ai bien lu le lien que j'ai envoyé précédemment et je crois avoir enfin compris ! Enfin !

Il existe 2 types de modulo, le modulo qui s'applique (excuse-moi pour ce terme mais il me semble adapté) à une égalité (=) mais qui va du coup se transformer (magie !) en une relation de congruence (;)). Car [n] s'utilise uniquement sur une relation de congruence. Cette relation possède donc un opérateur "binaire", si on utilise ;), il faut penser à [n] et vis versa.

Et le modulo du genre a mod b, ou encore a (mod b) ou MOD(a, b), qui retourne le reste de la division euclidienne de a par b.

Voilà voilà, je crois que c'est cohérent.

PS : pourquoi alors utiliser ;) et non pas = ?? La question a aussi été posée sur le lien de ma précédente réponse.

[Nightmare]

Contrairement à ce que tu sembles croire, la notion de congruence n'est pas très difficile à appréhender. Ce qui l'est un peu à la limite, ce sont les notations.

Les congruences, ça vient d'un principe simple : Quand on veux comparer les choses, il est souvent utile de les classer selon des critères. Alors ensuite, on dira que deux choses sont identiques quand elles vérifient les même critères.

Par exemple, si l'on étudie la taille des adultes Français, tout les français qui seront de même tailles seront "identifiés" entre eux dans l'étude. On aura alors plusieurs classes de Français : Ceux qui mesurent 1m70, ceux qui mesurent 1m80, ceux qui mesurent 1m68, etc...

Ce principe se retrouve aussi en maths. Quand on étudie les nombres, il est souvent utile d'en mettre certains dans un même panier, puis de travailler sur ce panier tout entier au lieu de travailler sur chaque nombre séparément.

Lorsque l'on travaille avec la divisibilité, un des paniers utile qu'on peut créer est celui où l'on réunit tout ceux qui ont le même reste dans la division par un certain nombre. C'est ce que font les congruences : On dit que deux nombres sont congrus entre eux modulo n s'ils ont le même reste dans la division par n, ou de manière équivalente, si leur différence est divisible par n, mais c'est plutôt la première définition qu'il faut retenir (l'idéal étant bien sûr de retenir les deux et de comprendre pourquoi elles sont équivalentes).

Cette idée de paniers, ou plutôt de classes (c'est le nom mathématique exact) se retrouve un peu partout, et en particulier, chez les angles.

Tu dois savoir depuis tes premiers pas avec les angles, qu'un angle est défini à un tour près (à 2pi près). Autrement dit, si je prends un angle et que je lui rajoute 2pi, je retombe sur le même angle. De façon assez naturelle, on a alors envie de dire que tous les angles qui diffèrent de 2pi sont égaux, sauf qu'on dira "congru" plutôt que "égaux" (et on écrit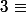 plutôt que =, pour ne pas confondre cette égalité entre des classes avec l'égalité usuelle entre les nombres)

Ainsi, si l'on écrit que 5pi = 3pi [2pi], c'est simplement parce que les deux angles de mesure 5pi et 3pi sont en fait les mêmes angles.

[Pixis]

Parce que ce ne sont pas les mêmes opérateurs :

= te donne une égalité, les termes de gauche et de droite sont égaux
;) te donne une congruence. Si tu écris 27=7 [5], ça n'a pas de sens : Ça voudrait dire 27 est égal à 7 crochet 5. En revanche 27;)7 [5] signifie que 27 est congru à 7 modulo 5, donc que 27 = k*5 +7 (ici k=4) ou, comme le dit nightmare, que 27 et 7 ont le même reste lors de la division euclidienne par 4

Mais la réponse de Nightmare me parait bien plus claire

[Tetdoss]

PARFAIT, merci beaucoup à vous, j'ai tout compris : mod est un opérateur et ;) [] en est un autre en quelque sorte, donc [n] ne peut pas s'utiliser seul de même pour ;) !

[Nightmare]

Ce ne sont pas vraiment des opérateurs, disons juste des notations.

[Pixis]

Ce ne sont pas vraiment des opérateurs, disons juste des notations.

En effet, je me suis mal exprimé

[Tetdoss]

De même pour moi, trop l'habitude de programmer en C++ :we:

[Nightmare]

Désolé, je répondais à Tetdoss en réalité, je n'avais pas vu que tu avais toi même employé ce mot.

Pour moi, opérateur = Application entre deux espaces structurées. (l'intégrale est un opérateur entre l'espace des fonctions et celui des réels, la racine carrée un opérateur entre les réels positifs, la dérivation un opérateur entre les fonctions etc.) Ici, on est pas vraiment en présence d'applications, au sens où l'on applique rien aux entiers (ou aux angles).

:happy3:

[Pixis]

C'est vrai, on devrait dans ce cas plutôt parler de symboles il me semble.

[Tetdoss]

Donc dans un contrôle de trigo par exemple, et que je dois déterminer ;), je peux très bien écrire par exemple :

;) = 2Pi + Pi ;) 3Pi (2Pi)

Il n'y aura aucun soucis ?

[Pixis]

Donc dans un contrôle de trigo par exemple, et que je dois déterminer ;), je peux très bien écrire par exemple :

;) = 2Pi + Pi ;) 3Pi (2Pi)

Il n'y aura aucun soucis ?


En soit c'est pas faux, mais il n'y a aucun intérêt à dire que 3Pi ;) 3Pi (2Pi)
Pour reprendre l'exemple de nightmare, c'est aussi utile de dire que Monsieur X à la même taille que lui même.

[Tetdoss]

Donc dans ce cas il ne faut pas écrire :

;) ;) 3Pi (2Pi)

mais

;) = 3Pi (2Pi)

? Ca remet un peu en cause ce qu'on a dit en disant que [n] s'utilise toujours avec ;) ...

[Pixis]

Non non non, si on te demande de trouver , c'est en effet par rapport à 2Pi, et il faut bien utiliser les congruences. Seulement, tu sais que si tu fais tourner quelque chose de zero radian, ça donnera la même chose que si tu le fais tourner de 2Pi radians, donc la même chose que si tu le fais tourner de 4Pi radians etc ... puisque 2Pi radian, ça fait un tour complet.

Maintenant, si tu as un angle de 7Pi, si tu lui enlève un tour complet, tu reviendras au même endroit, donc c'est en quelque sorte "équivalent" à un angle de 5Pi, lui même "équivalent" à un angle de 3Pi, encore une fois "équivalent" à un angle de Pi.
On dit donc que avec =7Pi on a Pi [2Pi]

Tu imagines bien un angle de Pi radian (equivalent à 180°) tandis que 7Pi, c'est moins facile à voir. Et pourtant, si tu fais une rotation de 7Pi, ça donnera la même chose qu'une rotation de Pi.

Pour résumer, le principer est de "faciliter" la lecture de l'angle, en trouvant un équivalent compris entre 0 et 2Pi.

Si je te demande de trouver b entre 0 et 2Pi tel que :

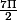
b [2Pi]

Tu me dis quoi ?