Incohérence

[wuuw]

On prend un nombre x=0.9999999 (etc)

Donc 10x=9.999999 (etc)
10x-x = 9x = 9
Donc x=1
Finalement 0.99999 =1

Alors? :id:

[Kikoo <3 Bieber]

On prend un nombre x=0.9999999 (etc)

Donc 10x=9.999999 (etc)
10x-x = 9x = 9
Donc x=1
Finalement 0.99999 =1

Alors? :id:

0,99999...=1
Alors là tu as manqué trois éléments : la virgule au lieu du point (sachant que l'on est francophones) les trois petit points indispensables car sinon l'égalité est fausse, puis enfin il ne s'agit pas d'une incohérence comme tu semblerais le croire.
Puis peut-être as-tu manqué un quatrième point : Comment arrives-tu de 10x-x=9x à 9x=9 ???
Il faudrait supposer que x=1 ce que tu n'as pas encore prouvé à ce stade...

[homeya]

Bonsoir,

L'expression 0,9999999 (etc) n'est pas un nombre réel au sens habituel mais une limite. En effet:
0,999999 (etc) = 0,9(10^(-1)+10^(-2) + ... + 10^(-n)) pour n tendant vers l'infini. Dans la parenthèse, il s'agit de la somme d'une suite géométrique de raison 10^(-1) et de premier terme 10^(-1). Il vient alors: 0,9(10^(-1)+10^(-2) + ... + 10^(-n)) = 0.9x10^(-1)(1-(10^(-1)(^n+1))/(1-10^(-1)) = 1x(1-(10^(-1))(n+1)). Cette expression tend vers 1 lorsque n tend vers l'infini.

Cordialement.

[Anonyme]

Le problème vient qu'on ne peut pas écrire x=0,999999......
car ce n'est pas un nombre qui existe !

sinon ton raisonnement et tes calculs sont justes car on aurait bien 10x-x = 9
car 9,99999... - 0,999999.... = 9

[Sylviel]

Pas d'incohérence. 1 à deux expressions décimales, dont une impropre...

[beagle]

Une approche intuitive pour dire qu'on parle du mème nombre est de dire:
entre deux nombres différents je peux toujours retrouver d'autres nombres,
ne serait-ce que somme des 2 divisée par deux, le milieu,
Mais là on va se positionner où pour planter un truc entre les deux?
S'il existait , suffirait de repousser les 9 un peu plus loin pour l'éloigner, et effectivement cela éloigne à jamais,...
C'est proche de la notion de limite j'imagine de le voir ainsi.

[Sylviel]

@ Beagle : non en fait tu es entrain de dire que ces deux nombres ne sont pas séparables, or R est un espace séparé donc ce sont les mêmes nombres.

[beagle]

@ Beagle : non en fait tu es entrain de dire que ces deux nombres ne sont pas séparables, or R est un espace séparé donc ce sont les mêmes nombres.

euh, je voulais dire,
si c'était deux nombres différents, alors il existerait un (ou plusieurs) nombres entre les deux.
Comme on ne peut pas trouver de nombres entre les deux, c'est qu'ils sont le mème nombre,
un seul nombre,
avec les deux écritures qui disent, nomment le mème nombre.

[Sylviel]

yep j'ai bien compris :-) et c'est juste. Je te donnais juste la terminologie de ce à quoi ça se rapporte (enfin c'est proche de l'idée de limite quand même ^^).

[beagle]

Il y a de nombreux fils consacrés à ce sujet.
Et plusieurs présentations possibles, de très mathématiques à plus intuitives.
Perso l'argument de l'absence de nombres possibles entre les deux m'avait bien plu.

Je n'aime pas beaucoup les multiplications et soustraction de nombres avec un nombre infini de chiffres, parce que ne connaissant pas ce que l'on peut faire avec les p-adiques, il me choque que la somme de nombres positifs plus grands que 1 soit au final une fraction négative plus petite que 1 pour prendre un exemple.
Comme c'est déconcertant, je ne peux admettre d'accepter un raisonnement qui dans d'autres circonstances me trouble.Donc je peux pas accepter le raisonnement du début de fil.

[Anonyme]

@tous
On est tous d'accord pour dire (de façon plus ou moins compliqué) que l'erreur dans le raisonnement est d'écrire l'égalité x=0.9999999....

On peut écrire que x ~ 0.9999999
mais cela change tout et on ne peut plus conclure que 1= 0.9999999....

[Sylviel]

Non ptinoir. Il n'y a pas d'erreur dans le raisonnement. Si on entends bien que 0,999... signigie une infinité de 9 après 0. Cela peut se réécrire comme 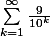et cela vaut bien 1. Si mes souvenirs sont bons c'est ce qu'on appelle l'expression impropre de 1.

[Alannaria]

Non ptinoir. Il n'y a pas d'erreur dans le raisonnement. Si on entends bien que 0,999... signigie une infinité de 9 après 0. Cela peut se réécrire comme et cela vaut bien 1. Si mes souvenirs sont bons c'est ce qu'on appelle l'expression impropre de 1.

En fait, on peut ajouter que les nombres décimaux ont deux développements décimaux: l'un propre, l'autre impropre avec une infinité de "9" (cette existence des développements décimaux impropres permet la connexité de la droite d'après le fameux paradoxe révolu car déjà résolu de l'époque d'un Zénon d'Elée).

J'adore quant à moi ces lapsus en quantité: signifie/signigie et origine/orgigine évocateurs d'une réalité !

[Anonyme]

@Sylviel
OK pour cette écriture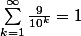

Faut il encore savoir l'interpréter correctement :

Questions

1) C'est un calcul d'une limite d'une série convergente ?

2) Pour démontrer ce résultat : il y a 2 solutions ?
soit le théorème des gendarmes
soit la formule de la somme des n premiers termes d'une suite géométrique , puis le calcul d'une limite quand n tend vers +infini

[Sylviel]

Oui calcul de série convergente, et c'est bien la limite des sommes partielles. Il y a plusieurs méthodes pour le faire, la plus simple étant -à mon avis- effectivement l'expression des sommes partielles et le passage à la limite.

[Anonyme]

Alors on peut écrire que 0.99999...... = 1 ?
ou faut-il plutôt éviter ?

[Sylviel]

On peut l'écrire. Cela ne sers qu'à faire prendre conscience de certaines choses (des limites, de l'existence de l'expression impropre de certains réels etc...), mais c'est possible.

[Alannaria]

On peut l'écrire. Cela ne sert qu'à faire prendre conscience de certaines choses (des limites, de l'existence de l'expression impropre de certains réels etc...), mais c'est possible.

On peut aussi dire à l'haut et fort que le côté impropre n'est pas là où on le situe d'emblée (Cf. intégrale).

[Anonyme]

Merci, Sylviel , pour tes explications supplémentaires qui m'ont permis de comprendre