Formules trigonometriques+limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Silvia90
- Messages: 9
- Enregistré le: 23 Déc 2008, 16:57
-
 par Silvia90 » 09 Nov 2009, 18:12
par Silvia90 » 09 Nov 2009, 18:12
Bonsoir! J'essaie depuis un bon moment de résoudre cet exercice, sans succès. J'ai la correction (pas très détaillée) mais je ne comprends quand même pas. Est-ce que vous pourriez m'aider s'il vous plaît?
)
f(x) étant:
Arctg(1/x^4)}{(1-cos(x))^2})
Merci d'avance!
silvia
-
mathelot
 par mathelot » 09 Nov 2009, 21:43
par mathelot » 09 Nov 2009, 21:43
Silvia90 a écrit:Bonsoir! J'essaie depuis un bon moment de résoudre cet exercice, sans succès. J'ai la correction (pas très détaillée) mais je ne comprends quand même pas. Est-ce que vous pourriez m'aider s'il vous plaît?
)
f(x) étant:
Arctg(1/x^4)}{(1-cos(x))^2})
Merci d'avance!
silvia
Dans le calcul de limite, on peut remplacer par des équivalents:
 \sim (x^2)^2)
)^2 \sim (\frac{x^2}{2})^2)
et a
)
par la formule exacte
)
-
Silvia90
- Messages: 9
- Enregistré le: 23 Déc 2008, 16:57
-
 par Silvia90 » 10 Nov 2009, 14:44
par Silvia90 » 10 Nov 2009, 14:44
En faisant comme cela je trouve bien
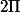
Mais dans les réponses du livre, la marche à suivre est plutôt celle-ci:
^2(\frac{x/2}{sinx/2})^4 arctg(1/x^4)= 2\Pi)
Or je ne comprends pas comment ils ont fait?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 10 Nov 2009, 15:08
par benekire2 » 10 Nov 2009, 15:08
Une question, en quelle classe est tu ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 10 Nov 2009, 15:51
par Skullkid » 10 Nov 2009, 15:51
Salut, ta démonstration est correcte (bien qu'il est inutile de modifier l'expression de l'arctan, vu que sa limite est directement calculable).
Visiblement la correction est destinée à des élèves qui n'ont pas étudié les équivalents, qui sont une notion "avancée" :
^2} = \frac{\sin^2 x^2}{x^4} \frac{x^4}{(1-\cos x)^2} Arctan \frac{1}{x^4})
Et on peut conclure par les limites dites classiques (qui ne sont en fait rien d'autre que les équivalent de base) : sin x / x tend vers 1 en 0, et (1-cos x)/x² tend vers 1/2 en 0. (Dans ta correction, ils redémontrent cette deuxième limite classique en utilisant la formule 1 - cos x = 2 sin² (x/2))
-
Silvia90
- Messages: 9
- Enregistré le: 23 Déc 2008, 16:57
-
 par Silvia90 » 10 Nov 2009, 18:29
par Silvia90 » 10 Nov 2009, 18:29
benekire2 a écrit:Une question, en quelle classe est tu ?
En fait je n'habite pas en France... mais en Suisse. Je pense que mon niveau correspondrait à terminale scientifique. :hein:
Pourquoi la question?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 10 Nov 2009, 18:30
par Timothé Lefebvre » 10 Nov 2009, 18:30
Salut,
parce qu'il est jaloux qu'on ne voit pas ça au Lycée en France :P
-
Silvia90
- Messages: 9
- Enregistré le: 23 Déc 2008, 16:57
-
 par Silvia90 » 10 Nov 2009, 18:34
par Silvia90 » 10 Nov 2009, 18:34
Skullkid a écrit:Salut, ta démonstration est correcte (bien qu'il est inutile de modifier l'expression de l'arctan, vu que sa limite est directement calculable).
Visiblement la correction est destinée à des élèves qui n'ont pas étudié les équivalents, qui sont une notion "avancée" :
^2} = \frac{\sin^2 x^2}{x^4} \frac{x^4}{(1-\cos x)^2} Arctan \frac{1}{x^4})
Et on peut conclure par les limites dites classiques (qui ne sont en fait rien d'autre que les équivalent de base) : sin x / x tend vers 1 en 0, et (1-cos x)/x² tend vers 1/2 en 0. (Dans ta correction, ils redémontrent cette deuxième limite classique en utilisant la formule 1 - cos x = 2 sin² (x/2))
Et bien je suis une élève qui n'a pas (encore ?) étudié les équivalents! (mais ils m'ont l'air bien pratiques)
J'ai justement essayé d'utiliser cette formule: 1 - cos x = 2 sin² (x/2)) mais je ne sais pas quoi faire du carré.
Bon je ne suis pas sure d'avoir assez d'éclaircissements pour comprendre la correction :mur: mais je vais essayer.
Merci!
-
mathelot
 par mathelot » 10 Nov 2009, 18:52
par mathelot » 10 Nov 2009, 18:52
Bj,
redémontrons
sur le cercle trigonométrique d'origine
)
,
;sin(x)))
pour
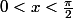
on obtient visuellement:
 \leq corde(AM) = \sqrt{2-2cos(x)} \leq x)
d'où
}{x}=1)
par composition avec la fonction carrée
}{x^2}=1)
par changement de variable bi-continu
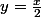
:
}{x^2}=1)
etc..
-
Silvia90
- Messages: 9
- Enregistré le: 23 Déc 2008, 16:57
-
 par Silvia90 » 11 Nov 2009, 19:59
par Silvia90 » 11 Nov 2009, 19:59
Je crois que cette fois c'est tout compris. Un grand merci pour votre aide! :happy2:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Nov 2009, 20:00
par benekire2 » 11 Nov 2009, 20:00
Timothé Lefebvre a écrit:Salut,
parce qu'il est jaloux qu'on ne voit pas ça au Lycée en France

Exactement !! C'est injuste, la France est minable la dessus.....
nous c'est sinx/x au maximum ...
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Nov 2009, 21:13
par Skullkid » 11 Nov 2009, 21:13
Heu, en quoi c'est minable de ne pas apprendre des concepts trop tôt ? Bidouiller une expression et la transformer, c'est utile pour d'autres trucs que le calcul de limite, et je trouve ça bien qu'en France on nous entraîne - ou tout du moins on essaye de nous entraîner - à ça.
C'est sûr y pourraient nous enseigner la super règle de l'Hospital qui nous apporterait taaaant...
Et soit dit en passant, dire que sin x / x tend vers 1 en 0, c'est exactement la même chose que dire que sin x est équivalent à x en 0, la deuxième façon est juste plus pédante.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
)