exercices puissances [4ème] - Forum Collège et Primaire

Rechercher sur Maths-Forum

		Maths-Forum > Forum Soutien scolaire en mathématiques > Forum Collège et Primaire
exercices puissances [4ème]

Outils de la discussion

Rechercher

Modes d'affichage

10/01/2010, 11h37
busard_des_roseaux Membre Complexe Sur Maths-Forum depuis: septembre 2007 Messages: 3 291	exercices puissances [4ème] Bonjour, en vue de préparer un contrôle, cherche exercices de 4ème sur les puissances (exposants négatifs) difficiles. merci Dernière modification par busard_des_roseaux 10/01/2010 à 16h23.

10/01/2010, 11h42

Sve@r

Membre Complexe

Sur Maths-Forum depuis: avril 2008

Localisation: Creil

Messages: 5 575

Citation:

Posté par busard_des_roseaux

Bonjour,

en vue de préparer un contrôle, cherche exercices de 4ème sur les puissances
(exposants négatifs) difficiles.

merci

Boaf, laissons libre cours à notre imagination. Moi je propose déjà $2^{-2}^{-2}$ ...

__________________

Règlement du forum
Message important de la modération
Traceur de courbes
Comment écrire des formules
Comment insérer une image

10/01/2010, 12h28
busard_des_roseaux Membre Complexe Sur Maths-Forum depuis: septembre 2007 Messages: 3 291	les exposants fractionnaires ne sont pas au programme

10/01/2010, 13h20
oscar Membre Complexe Sur Maths-Forum depuis: février 2007 Localisation: Belgique: Huy Messages: 10 501	a ^ -n = 1/a^ n a) Calcule 3^ -2; ( 1/2) ^ -1; (2/3) ^ -2 , ( -1/10) ^ -3 b) Ecris les expressions suivantes aec des exposantq positifs 1)5a²* b ^-3 = 5a² /b³ 2) a³ * b-5 3)a ^ -2 * b ^ -5 4) 2 a^ 3/ b ^ -2

10/01/2010, 16h40
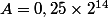
busard_des_roseaux Membre Complexe Sur Maths-Forum depuis: septembre 2007 Messages: 3 291	en voilà que j'ai rédigé pour la classe de 4ème bonsoir, finalement, en voilà, que j'ai bricolés: *exercice 1 [Puissances de 2]* écrire le résultat comme une puissance de 2: $\displaystyle A=0,25 \times 2^{14}<br />$ $\displaystyle B=\frac{0,01}{(0,5)^{ -3} \times 5^{-2}}$ *exercice 2 [écriture scientifique]* indiquer l'écriture scientifique de: $\displaystyle C=1234567 \times 10^{(-2)^3}$ hint: commencer par calculer cet exposant bizarroïde $\displaystyle D=\frac{31 \times 10^{-2} +415,9 \times 10^{-5}}{10^{-1}}$ *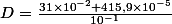exercice 3 [écriture scientifique]* ranger par ordre croissant les nombres e,f,g $\displaystyle e= 968 \times 10^6$ $\displaystyle f = 0,00621 \times 10^{14}$ $\displaystyle g= 32,21 \times 10^9$ 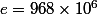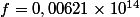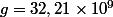hint: les écrire en notation scientifique *exercice 4 [quotient]* écrire sous forme simplifiée $\displaystyle H=\frac{8 \times 10^{15} \times 15 \times 10^{-6}}{20 \times (10^2)^5}$ hint: simplifier avant d'effectuer remarque: $2^{-2^{-2}}=\frac{1}{\sqrt[4]{2}}$ 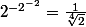c'est le nombre positif qui, élevé à la puissance 4 , donne $\frac{1}{2}$ en effet $\left( 2^{-2^{-2}} ) ^4 = 2 ^{- 2^{-2} \times 2^2}=2^{-2^0}=2^{-1}=\frac{1}{2}$ Dernière modification par busard_des_roseaux 10/01/2010 à 16h53.

10/01/2010, 17h05

Sve@r

Membre Complexe

Sur Maths-Forum depuis: avril 2008

Localisation: Creil

Messages: 5 575

Citation:

Posté par busard_des_roseaux

remarque:

$2^{-2^{-2}}=\frac{1}{\sqrt[4]{2}}$

c'est le nombre positif qui, élevé à la puissance 4 , donne $\frac{1}{2}$

Arf, je me suis mal exprimé. J'ai pas écrit $2^{(-2^{-2})}$ mais $2^{-2}^{-2}$ . Il me semble que, puisqu'il n'y a pas de parenthèses, on calcule en fait $(2^{-2})^{-2}$ ce qui donne $2^{(-2) \time (-2)}=2^4$ ...

__________________

Règlement du forum
Message important de la modération
Traceur de courbes
Comment écrire des formules
Comment insérer une image

10/01/2010, 17h21

busard_des_roseaux

Membre Complexe

Sur Maths-Forum depuis: septembre 2007

Messages: 3 291

Citation:

Posté par Sve@r

Arf, je me suis mal exprimé. J'ai pas écrit 2^{(-2^{-2})} mais 2^{-2}^{-2}.

exact, c'est LaTex qui interprète.La deuxième écriture est ambigüe
mais se lit habituellement de droite à gauche:

a^b^c signifie a^{b^c} parce que l'autre possibilité s'écrit simplement a^{bc}

mais effectivement pour les informaticiens

c'est illogique.

Dernière modification par busard_des_roseaux 10/01/2010 à 17h29.

10/01/2010, 17h29

Sve@r

Membre Complexe

Sur Maths-Forum depuis: avril 2008

Localisation: Creil

Messages: 5 575

Citation:

Posté par busard_des_roseaux

Je comprends alors pourquoi t'as parlé d'exposant fractionnaire. Mais mon idée était effectivement que l'exercice soit de réduire (a^b)^c en a^(bc) avec a, b et c un peu difficiles...

__________________

Règlement du forum
Message important de la modération
Traceur de courbes
Comment écrire des formules
Comment insérer une image

10/01/2010, 17h35
busard_des_roseaux Membre Complexe Sur Maths-Forum depuis: septembre 2007 Messages: 3 291	re, je demande à la calculatrice TI89 de calculer 2^5^2 elle renvoie 33554432 et non pas 1024. ça oblige à écrire 1024=(2^5)^2 en effet, si T est une opération aT b T c = (a T b) T c pour pratiquement toutes les opérations sauf l'exponentiation (exception qui confirme la règle) Dernière modification par busard_des_roseaux 10/01/2010 à 18h10.

10/01/2010, 19h36

Sve@r

Membre Complexe

Sur Maths-Forum depuis: avril 2008

Localisation: Creil

Messages: 5 575

Citation:

Posté par busard_des_roseaux

re,

je demande à la calculatrice TI89 de calculer

2^5^2

elle renvoie 33554432 et non pas 1024.

J'ai pas de calculatrice sci sous la main. Je regarderai demain au bureau. Mais effectivement, quand j'ouvre une invite de commande Python et que je demande 2**5**2 j'obtiens aussi 33554432.

Citation:

Posté par busard_des_roseaux

aT b T c = (a T b) T c pour pratiquement toutes les opérations
sauf l'exponentiation (exception qui confirme la règle)

Ok, une exception que je ne connaissais pas. Mais on va revenir à ma proposition où je proposais simplement $(-2^{-2})^{-2}$ quoi. Mais tu as posé un truc qui s'en approche dans ton C.

__________________

Règlement du forum
Message important de la modération
Traceur de courbes
Comment écrire des formules
Comment insérer une image

Dernière modification par Sve@r 10/01/2010 à 19h39.

Outils de la discussion	Rechercher
Afficher une version imprimable Envoyer un lien vers cette page par email	Rechercher: Recherche avancée
Modes d'affichage
Mode linéaire Choisir le mode hybride Choisir le mode arborescent

Discussions similaires
Discussion	Forum	Réponses	Dernier message
2 exercices "infaissable"	Forum Collège et Primaire	4	27/10/2010
Exercices 4ème.	Forum Collège et Primaire	6	19/05/2010
Exercices d'inéquation	Forum Collège et Primaire	2	12/11/2008
Vérifiez mes exercices...	Forum Collège et Primaire	2	13/09/2008
3 exercices de géomètrie	Forum Collège et Primaire	15	12/05/2008
2 Exercices	Forum Collège et Primaire	4	11/05/2008
Correction exercices triangle rectangle	Forum Collège et Primaire	6	04/05/2008
Puissances [4ème]	Forum Collège et Primaire	12	01/03/2008
2 Exercices difficiles de D.T.L	Forum Collège et Primaire	4	20/02/2008
Exercices sur les puissances	Forum Collège et Primaire	1	24/01/2008
2 exercices sur les puissances	Forum Collège et Primaire	3	12/05/2007
plusieurs exercices à rendre	Forum Collège et Primaire	1	23/04/2007
[DM] Mathématiques : Puissances : 2 exercices.	Forum Collège et Primaire	1	25/02/2007
Corriger mes exercices	Forum Collège et Primaire	7	23/02/2007
DM sur les puissances :-s	Forum Collège et Primaire	4	05/01/2007

Règles des messages du forum de mathématiques
Vous pouvez ouvrir de nouvelles discussions : nonoui Vous pouvez envoyer des réponses : nonoui Vous pouvez insérer des pièces jointes : nonoui Vous pouvez modifier vos messages : nonoui Les balises BB sont activées : oui Les smileys sont activés : oui La balise [IMG] est activée : oui Le code HTML peut être employé : non