Espace vectoriel

[manianga]

bonjour

je bloque sur un exercice qui me demande de montrer que l'ensemble des fonctions solutions de l'équation differentielle y''(t²)+y(t)=0 est un espace vectoriel sur R

je ne comprend pas comment on peut le prouver

merci de votre aide

[pedro_cristian]

Ecrire la définition d'un espace vectoriel et essayer de prouver toutes les affirmations de cette définition pour les solutions de l'equadiff.

[BQss]

bonjour

je bloque sur un exercice qui me demande de montrer que l'ensemble des fonctions solutions de l'équation differentielle y''(t²)+y(t)=0 est un espace vectoriel sur R

je ne comprend pas comment on peut le prouver

merci de votre aide

Resoud l'equadiff.
Tu vas trouver une somme de deux fonctions chacune multiplié par une constante. A ce moment là tu fais comme pedro a dit et tu demontres que cet ensemble possede les propriétés d'un espace vectoriel (c'est super simple a faire vu que tu as montré que tout ses elements se mettaient sous une forme "ax+by" avec a et b des variables de IR, x et y les vecteurs de ta base)...
Tu as deja l'element neutre de l'addition par exemple en posant k1=0 et k2=0 ... Represente toi un espace vectorielle en dimension un par une droite qui passe par l'origine en dimension deux(comme ici) par un plan qui passe par l'origine.

[abcd22]

Resoud l'equadiff.

C'est inutile ici. Dans ce que tu dis dans la suite du message tu utilises des résultats qui viennent justement de la structure d'espace vectoriel de l'ensemble des solutions...

[yos]

Resoud l'equadiff.

D'ailleurs est-ce qu'elle se résout "simplement"?

[BQss]

D'ailleurs est-ce qu'elle se résout "simplement"?

j'avais vu y''(t) a la place de t^2, donc non elle ne se resout pas facilement.


quand a l'autre post sur le fait qu'on a pas besoin de resoudre, il n'y a effectivement pas besoin de la resoudre.

Sauf que dans le cas precis(y''(t)) que j'avais cru voir au lieu de y''(t^2).

C'est immediat et evident.

Car tu sais que la solution de ce type d'equation est du type kg(x) + k'h(x) (resultat connu) c'est a dire quelquechose qui se met sous la forme de la somme de deux fonctions fois deux constantes et ca, c'est la forme generale de l'ecriture des elements d'un espace vectoriel de dimension 2.


Le fait qu'elle s'ecrive comme ca ne decoule pas du fait que ce soit un espace vectoriel mais du fait que ce soit un espace vectoriel de dimension 2 et meme si tout cela est lié ce n'est pas la meme methode.

Dans le cas trivial y"(t) on met le resultat sous une ecriture familiaire et l'on reconnait celle d'un espace vectoriel. Il n'y a plus qu'a verifié qu'un ensemble d'elements qui s'ecrivent xu + yv est un espace vectoriel, qui est normalement meme un resultat admis....

Dans l'autre y"(t^2) tu n'as pas mis en evidence une ecriture des solutions, et tu dois verifier une a une les propriétés a partir de l'equation. C'est pas tres dure non plus mais c'est moins rapide que la premiere methode dans le cas d'une equation differentielle connu(c'est une question de methode, ce que je disais n'etait pas redondant car avec y"(t) je connaissais deja la forme generale des solutions...), ou on sait deja la forme des solutions... Ce raccourci aurait permis dans le cas y"(t) d'aller bcp plus vite. Ce n'est pas une question de "necessaire ou pas" mais de "plus rapide ou pas"(montrer qu'un ensemble d'elements qui s'ecrivent ux+yv est un espace vectorielle c'est tres tres rapide et simple...)

Ca s'appelle du pragmatisme:

E l'ensemble des (i| i=xu+yv) --> E est un espace vectorielle
E est un espace vectoriel n'entraine pas i=xu+yv(dimension 2?, stable?, ensemble vide?).

Comme la premiere methode dans le cas y"(t) est plus rapide, je conseille de l'employer. Bon la c'est y"(t^2), mais le probleme n'est pas de dire "c'est pareille de dire y=ux+vy et de montrer chaque propriété une a une", evidemment... C'est une question de methode si l'on connait certains resultat.

D'ailleurs, est ce que l'ensemble des solutions est un espace vectoriel de dimension 2? Tu pourrais me le prouver?;)

Et donc dans notre cas, la demonstration la plus rapide n'est evidemment pas de dire que les solutions sont de la forme X=somme(x(i)u(i)) car il faudrait le montrer et ca n'a aucun interet car cela reviendrait effectivement a montrer que c'est un espace vectoriel car ces questions sont equivalentes(a quelques nuances triviales pres)... Et c'est pour ca que je lui proposais de redemontrer chaque propriété d'un espace vectoriel a partir de cette ecriture, ca va plus vite si l'on sait deja que ca s'ecrit comme ca) c'est plus rapide de montrer que c'est un espace vectoriel si cela revient juste a montrer que des elements s'ecrivant sous forme d'une combinaison lineaire forment un espace vectoriel...


conclusion:

yos merci pour ton post j'avais mal vu.

abcd22, tu n'as pas compris le sens de mon intervention.

Moi, je lirais mieux la prochaine fois, ca evitera les posts inutiles et or sujet(les miens et ceux des autres pour certains.).

[abcd22]

Le fait qu'elle s'ecrive comme ca ne decoule pas du fait que ce soit un espace vectoriel mais du fait que ce soit un espace vectoriel de dimension 2 et meme si tout cela est lié ce n'est pas la meme methode.

Un espace vectoriel de dimension 2 n'est pas un espace vectoriel ?
Dans la démonstration du résultat que tu donnes on dit :
1) l'ensemble des solutions est un espace vectoriel,
2) il est de dimension 2 par le théorème de Cauchy (unicité) : une solution est entièrement déterminée par ,
3) on cherche 2 solutions linéairement indépendantes, elles forment une base car l'ensemble des solutions est de dimension 2.
Donc quand tu sors ce résultat pour démontrer que l'ensemble des solutions d'une équation différentielle homogène du second ordre est un espace vectoriel tu tournes en rond ! et en plus c'est vraiment écraser une mouche avec un marteau-pilon.

abcd22, tu n'as pas compris le sens de mon intervention.

Dans tous les cas c'est plus rapide de montrer directement que l'ensemble des solutions contient 0 et est stable par combinaison linéaire que de chercher à résoudre l'équation, si tu as besoin de passer par l'écriture explicite des solutions pour trouver ça évident c'est toi qui n'as vraiment pas compris ce qu'est un espace vectoriel (en L1 voire L2 ça peut se comprendre, en master on est censé avoir un minimum de recul là-dessus quand même).

[BQss]

Oula oula on se calme.
Je n'ai pas de temps a perdre alors je serais le plus laconique possible(rude tache pour ceux qui me connaissent).

Dans tous les cas c'est plus rapide de montrer directement que l'ensemble des solutions contient 0

C'est insuffisant, revois ton cours. Cela serait suffisant si tu savais que cet espace etait inclu dans un autre espace vectoriel, mais tu n'as pas montré cela(ou alors montre le, c'est pas tres dure mais il faut le faire, je te propose d'introduire l'espace vectorielle C2, elle est de clase C2 vu que y"(t^2) est egal a une fonction deux fois derivable et donc continue...).
Tu dois redemontrer une a une les propriétés d'un EV, c'est a dire qu'il faut encore enumerer (meme si c'est debile je te le concede) les propriété de la loi externe et rapeller que c'est bien associatif pour +, meme si c'est clair vu qu'on manipule le groupe (R,+) ou alors dis le. Et c'est evidemment plus rapide de montrer que ku + k'v forme un espace vectoriel que de demontrer cela a partir de l'equa diff( ce n'est pas une question de facilité). Ici c'est different de toute facon ce n'est pas y"(t) mais y"(t^2).
La difference est simple et c'est la que tu butes. Dans le cas rapide (pour y"(t) ) il suffit de montrer que la combinaison lineaire met en evidence un EV(il faut prouver juste cela pour une combinaison lineaire, sachant qu'on sait que les resultats sont comme cela), dans l'autre methode il faut prouver que c'est un EV en utilisant l'equadiff! J'espere que tu vas comprendre la. Et donc dans cette methode on a pas le droit de poser que les solutions sont de la forme ( somme x(i)u(i) ) (ce qui ne revient pas exactement a dire que l'espace est vectoriel, donc il reste quand meme un peu a faire), car la forme generale des solutions de l'equa diff n'est pas connu. J'ai encore l'espoir que tu saisisses la nuance( evidemment que les elements d'un espace vectoriel peuvent se mettrent sous forme d'une combinaison lineaire, le truc que tu ne comprends pas c'est que pour y"(t) dans ma methode il faut le montrer mais plus besoin de l'equa diff!(faut bien montrer quelquechose une fois que l'on a rappelé le resultat) alors que l'autre methode vu qu'on utilise pas cette expression "equivalente" on se contre fout de cette ecriture sous forme de combinaison lineaire et on montre connement les propriété une a une, implicitement evidemment cela revient a dire que les elements s'ecrivent sous forme d'une combinaison lineaire mais la n'est pas le sujet! Le probleme de cauchy n'est absolument pas equivalent a dire que les resultats forme un EV, il conjecture juste sur la dimension n de l'ensemble des solutions quand l'equation( y(t)...y(n)(t)) est de dimension n. Dire que n conditions suffisent ca ne veut evidemment pas forcement dire qu'il s'agit d'un EV de dimension n. Tu admets que c'est un espace vectoriel en "1)" tu l'as prouvé ou? pour y(t) on le sait mais pour y(t^2) on ne connait pas la forme des solutions, ma methode ne marche pas pour y(t^2).

Je peux t'inventer des miliers d'ensembles determiné uniquement a partir de deux points qui ne sont pas des espaces affines et encore moins vectoriel. L'ensemble des fonctions f(x)=K/(K-1+x)+ K'/(K'-1+x) par exemple n'est pas un EV sur R, pourtant il est entierement determiné par deux points et il contient l'element neutre 0 de l'addition. En dimension 1, l'ensemble k/(k+1) K appartient a R, ou un element est entierement determiné par k donc un point, pourtant ce n'est pas un EV pour "+". Pour t'en convaincre k/(k+1)+k/(k+1)=2K/k+1; si k=2 par exemple cela vaut 3/2 or k/(k+1) ne peut etre superieur a 1 et donc cet ensemble n'est pas stable pour + malgré qu'une condition et seuleument une seule suffise a choisir un de ces elements...
L'ensemble des mecs bidons en maths qui sont uniquement ami avec une personne et ont un chien de race(aucun n'ayant a la fois la meme race de chien et le meme ami) n'est pas non plus un espace vectoriel . Mais une fois que je connais la race du chien et l'ami, j'ai determiné mon mec bidon.
Pourtant ces mecs bidon la ne forme absolument pas un espace vectoriel de mec bidon, il n'y a meme pas d'operation la sur ces mecs bidons et encore moins une base de dimension 2 commune malgré que la connerie soit universelle . Ces mecs bidons ne forme evidemment pas un EV (meme si créer une combinaison lineaire sur les réels est possible) mais elle sera de toute facon pas stable .
Je ne vois donc pas pourquoi on admettrait que c'est un EV, sauf si comme pour y(t) on connait la forme generale des solutions.

si tu as besoin de passer par l'écriture explicite des solutions pour trouver ça évident c'est toi qui n'as vraiment pas compris ce qu'est un espace vectoriel

Oula, calme toi, car tu commences a delirer la . Je dis que c'est plus rapide, pas une question d'evidence ou de besoin. C'est effectivement plus rapide de dire directement que les solutions de y"(t)+y(t)=0 sont de la forme kf(x)+k'g(x)(resultat connu) et donc de montrer que c'est bien un espace vectoriel, sachant que ici k et k' sont des réels...

Ici c'est different c'est y"(t^2) rien a voir, aucun resultat connu la dessus, il faut donc redemontrer si tu veux utiliser la forme "combinaison lineaire"... Ici il faut passer par l'equa diff et prouver les resultats un a un, ca prendra 5 minutes au lieu de 2(dans le cas y"(t) on a juste a prouver que cette combinaison lineaire et bien celle des elements d'un espace vectoriel ), voila tout.

Un espace vectoriel de dimension 2 n'est pas un espace vectoriel ?

Apparemment tu aimes bien t'inventer des interlocuteurs en leur attribuant des idioties, ca te permet de t'elever au dessus de quelquechose d'assez bas, ce qui est parfait dans ton cas, cela realise le compromis de ton orgueuil et de tes connaissances... Je vais t'epargner la psychologie de comptoir et ne pas te dire ce que je pense des gens qui font cela ou encore eviter d'epiloguer sur les complexes qui sont subbordonnées a ce genre d'attitude.
Tu n'as toujours pas compris le sens de ce que je disais... Mais tu peux discuter avec toi meme si tu le desires, tu auras le choix de debattre sur les debats les plus absurdes qu'il soit et a ta guise.

3) on cherche 2 solutions linéairement indépendantes, elles forment une base car l'ensemble des solutions est de dimension 2.
Donc quand tu sors ce résultat pour démontrer que l'ensemble des solutions d'une équation différentielle homogène du second ordre est un espace vectoriel tu tournes en rond ! et en plus c'est vraiment écraser une mouche avec un marteau-pilon.

Tu n'as toujours pas compris. Si tu l'avais je ne pense pas que tu aurais repondu d'ailleurs. Mais je te pardonne, que ce soit d'echecs, de basket ou de maths les forums sont remplis de gens comme toi qui ne cessent de repondre a coté. Cela fait longtemps que je ne pers plus mon temps a essayer de leur faire entendre ce qu'ils ne voudront jamais voir. C'est donc mon dernier message la dessus.

2) il est de dimension 2 par le théorème de Cauchy (unicité) : une solution est entièrement déterminée par (y(0),y'(0))

Tres bien de dimension 2, mais pas forcement vectoriel!

Bon ici en l'occurence c'est y" et pas y', ca ne change pas grand chose donc je ne t'en tiens pas rigueur.
Par contre c'est y"(t^2) et pas y"(t)

Le theorme de Cauchy est enoncé pour des fonction y(t) y'(t) y(n)(t) et pas pour des fonction y(t^a) y'(t^b) y"(t^c) (si tenté que ca est de l'importance vu que le probleme de cauchy comme je l'ai dit plus haut n'est absolument pas equivalent a dire que les solutions forme un espace vectoriel), si tu veux dire que les solutions de ces equations differentielles la, peuvent aussi etre mises sous la forme d'une combinaison lineaire, tu dois donc le prouver( le probleme c'est que la demonstration "niveau bac+1", donc j'espere que tu l'as connait, qui montre qu'une equation du second ordre de la forme A(y(t) y'(t) y"(t) )=0 possede une et une seule solution verifiant y(x0)=y0 et y'(x0)=y'(0), utilise justement le fait que l'on sait que les solutions sont de la forme ku +k'v, alors que toi tu poses le probleme a l'envers... Ici justement on ne sait pas la forme generale des solutions de ce type! Car c'est y"(t^2) et pas t, il ne suffit evidemment pas de dire, c'est le probleme de cauchy, tu melanges un peu tout la) ou alors utiliser des resultats qui ne sont absolument pas connu pour celui qui posait la question (a l'evidence cette question provient d'un bac+1) et donc pas utilisable(encore une fois un probleme de pragmatisme), alors que pour y"(t) +y(t)=0 la solution est bien connu et cela justifie de passer par la pour aller plus vite(http://www.les-mathematiques.net/a/d/c/node6.php3 ou http://ups.prepas.org/maths/progs/mp/mpanal4.html, un petit lien, ou l'on voit y"(t) et nulle part du y(n)o[f(t)])... C'est a dire qu'au lieu de montrer que c'est un espace vectoriel en se servant de l'equa diff, il suffit de montrer que c'est un espace vectoriel en sachant que ses elements s'ecrivent sous une combinaisons lineaires de deux vecteurs...(et c'est ca que tu ne comprends pas depuis le debut). Dans le cas y"(t)(et pas y"(t^2)) la deuxieme methode est plus rapide,meme si l'autre est courte aussi, la question n'est pas tres dure quelque soit la methode...

en L1 voire L2 ça peut se comprendre, en master on est censé avoir un minimum de recul là-dessus quand même).

j'espere que toi tu y es toujours ... Désolé si je t'ai vexé dans le precedent post en tout cas, mais tu en verras d'autre si tu restes sur la meme ligne...


Je te laisse le soin de faire le dernier post sur ce debat sans interet, ca a l'air de te tenir a coeur d'avoir le dernier mot , fusse t-il vain.

Je constate que j'ai echoué sur le laconique:D.

Bonne soirée .

[BQss]

Un espace vectoriel de dimension 2 n'est pas un espace vectoriel ?
Dans la démonstration du résultat que tu donnes on dit :
1) l'ensemble des solutions est un espace vectoriel,
2) il est de dimension 2 par le théorème de Cauchy (unicité) : une solution est entièrement déterminée par ,
3) on cherche 2 solutions linéairement indépendantes, elles forment une base car l'ensemble des solutions est de dimension 2.
Donc quand tu sors ce résultat pour démontrer que l'ensemble des solutions d'une équation différentielle homogène du second ordre est un espace vectoriel tu tournes en rond ! et en plus c'est vraiment écraser une mouche avec un marteau-pilon.

Je precise juste au passage que tu n'as rien compris a ma demo( pas etonnant que tu divagues apres...

3) on cherche 2 solutions linéairement indépendantes, elles forment une base car l'ensemble des solutions est de dimension 2.

N'importe quoi... Effectivement si tu ne vois pas qu'on a plus besoin d'utiliser l'equadiff une fois qu'on a mis en evidence cette ecriture c'est difficile a concevoir...

Ma demo(pour ay"(t)+cy(t) et pas y"(t^2)! ):

1)Cette equation diff est connu et les solutions sont de la forme C1exp(ux) + C2exp(vx)

2)Prouvons que si les solutions s'ecrivent y=C1exp(ux) + C2exp(vx) avec C1 et C2 des réels! alors les solutions forme un espace vectoriel sur R...
Mais il n'y a rien a prouver si C1,C2 sont réel car c'est l'ecriture des elements de EV de dim 2.
Ou alors tu peux le demontrer si tu aimes perdre du temps mais ca va plus vite encore qu'en passant par l'equa diff...


C'est a dire par exemple on prouve qu'on a bien si y1 s'ecrit comme ca alors ay1 s'ecrit comme ca.
Au lieu de passer par l'equa diff et de montrer que (pour cette propriété) si y1 est solutions alors ay1 est solution (biensur ca c'est si on a y"(t))...
Ou alors rassembler pas mal des propriété a demontrer dans une combinaison lineaire .

Avec y"(t^2) on est obligé de passer par l'equadiff par contre:
Soit y''(t²)+y(t)=0
(ay)"(t^2)=a(y")(t^2)=a( (y")(t^2)+y(t) ) -ay(t) = a*0 -ay(t)=-ay(t)
donc (ay)"(t^2) +ay(t)=0...

Ce qui est plus lent et encore moins trivial que (si l'on savait que ca s'ecrit comme ca, ce qui est le cas pour y"(t):
si y=C1e(ux) + C2e(vx) alors ay=aC1e(ux) + aC2e(vx)=C1'e(ux) + C2'e(vx)...

Dans tous les cas c'est plus rapide de montrer directement que l'ensemble des solutions contient 0 et est stable par combinaison linéaire que de chercher à résoudre l'équation, si tu as besoin de passer par l'écriture explicite des solutions pour trouver ça évident c'est toi qui n'as vraiment pas compris ce qu'est un espace vectoriel (en L1 voire L2 ça peut se comprendre, en master on est censé avoir un minimum de recul là-dessus quand même).

Outre le fait que ce soit insuffisant(soit tu utilises 0 comme un element quelquonque pour montrer que ce n'est pas vide et tu dois donc rajouter que c'est un sous espaces vectoriel des fonctions de classe C2(voir post d'avant), soit il te reste meme si c'est le plus trivial au monde a ennoncée que y=1y ou encore que on a bien(a+b)y=ay+by et les autres propriété de la loi externe(et ba ouai) .
Au final j'aime bien la methode par les fonctions de classe C2(y est meme 4 fois derivable et 3 fois continument dans l'exo) c'est encore plus rapide que la mienne pour y"(t)(l'autre etant plus longue et chiante, meme si c'est que 2 minutes de plus)...

Outre ca donc, j'espere que tu as compris que je parlais pas d'un besoin mais d'une solution plus rapide dans le cas de y"(t) car c'est ce que j'avais lu au depart?
Quand j'ai dit resoud, je parlais bien d'une equa diff connu, c.a.d met la sous sa forme explicite sachant que tu sais a quoi elle ressemble(et c'est pour ca que j'ai precisé sa forme au +bv, c'est un resultat connu, il n'avait evidemment pas besoin d'ecrire la solution exacte mais la forme generale seuleument...)...A partir du moment ou je lui donne la forme des solutions c'est que implicitement on a le droit d'admettre cette forme, et c'est a partir de cette forme qu'il fallait ensuite conclure... T'es sur que tu n'es pas enarque, parce que je vois mal un mathematicien qui s'obstine a ne pas comprendre et s'inventer en desespoir de cause des problemes qui n'ont jamais existés.


Allez assez perdu de temps a+...

[abcd22]

J'ai pas eu le courage de te lire mais tu t'enfonces visiblement... Comme si on n'était pas au courant que l'ensemble des fonctions de classe C2 sur un intervalle était un espace vectoriel et qu'on demandait de le démontrer à chaque fois qu'on l'utilise... On n'a même pas besoin de ça, il suffit de savoir que l'ensemble des fonctions (au départ de n'importe quel ensemble, donc ici on va dire fonctions à variables réelles définies sur un intervalle) à valeurs dans R ou C est un R ou C-espace vectoriel, ce qui vient de la structure de R-espace vectoriel de R, ou de C-espace vectoriel de C (ça fait partie des exemples d'espaces vectoriels de base qu'on voit en L1/maths sup).
Tu n'as toujours pas compris pourquoi l'ensemble des solutions d'une équa-diff linéaire homogène du second ordre à coefficients constants est l'ensemble des fonctions de la forme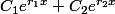 avec r1 et r2 racines de l'équation caractéristique. Recherche la démo dans tes cours de DEUG tu verras bien que ça utilise la structure d'espace vectoriel des solutions.

[BQss]

Comme si on n'était pas au courant que l'ensemble des fonctions de classe C2 sur un intervalle était un espace vectoriel et qu'on demandait de le démontrer à chaque fois qu'on l'utilise...

LOL encore a coté.
Je ne prouve nulle part que C2 est un espace vectoriel einstein, j'utilise justement ce resultat dans une autre demo que j'ai introduite au passage(voir ci dessous).
C2 ici ne sert qu'a definir un espace contenant l'ensemble des solutions. On ne peut pas definir un espace aussi "grand" que C^(0) dans cet demo car C^(0) dans cette demo ne contient pas les solutions.

Je te precise au passage que cen'est pas l'unique demo, pour eviter que tu redises, "mais on a pas besoin de savoir que c'est de classe C2). Lol oui monsieur on a pas besoin, mais ce n'est pas ce que je dis encore une fois...

J'ai pas eu le courage de te lire mais tu t'enfonces visiblement... On n'a même pas besoin de ça, il suffit de savoir que l'ensemble des fonctions (au départ de n'importe quel ensemble, donc ici on va dire fonctions à variables réelles définies sur un intervalle) à valeurs dans R ou C est un R ou C-espace vectoriel, ce qui vient de la structure de R-espace vectoriel de R, ou de C-espace vectoriel de C (ça fait partie des exemples d'espaces vectoriels de base qu'on voit en L1/maths sup).

Apparemment tu ferais bien d'aller chercher plus loin que le deug alors parce que tu racontes des enormités, enfin c'est juste une question de logique, ou peut-etre tu devrais mieux lire ce que j'ecris et ne pas te precipiter, ca t'evitera de repondre encore a coté.
Cette methode (tres tres simple) utilise le fait que l'ensemble des solutions est inclus dans un autre espace vectoriel. Mais lequel? Surement pas C0.
Tu as une equation avec du y" et tu me dis qu'on a pas besoin de definir l'espace vectoriel C2 pour cette methode la (regarde bien quel methode j'ai utilisé quand je parle de C2) mdr... L'ensemble de tes solutions "y" la einstein il est pas inclu dans C^(0). Tu as fait un peux d'equa diff apres la prepa? equa aux dérivées partielle, recherche de sol, element fini distribution des trucs comme ca, je pense pas...
Mais je te rassure ca se prouve vite que y appartient a C2 vu que si y"(t^2)+y(t)=0, alors comme y(t) est continue et que l'on cherche des solutions tel que y"(t^2)=-y(t) alors y" est aussi continue et donc y est de classe C2 et meme de classe C3 a vrai dire(prouve le moi tien que c'est de classe C3, c'est elementaire mais bon...).

Si tu utilies la methode que je suggerais, l'autre, celle ou j'ai introduit l'espace vectoriel C2(c'est a dire pas celle des combinaisons lineaires, la troisieme si tu veux l'appeler comme ca), tu dis ca(et c'est uniquement dans ce cadre la que je l'ai introduit C2, donc un conseil, lis bien concentre toi, ou abstiens toi de parler car tu es a chaque fois or sujet):
L'espace des solutions est inclu dans C2(preuve en haut) de plus il n'est pas vide car 0 appartient a l'espace(tu le montres) et stable pour +, or C2 est un espace vectoriel donc l'ensemble des solutions est un sous espaces vectoriel de C2 et donc un espace vectoriel, tu dois BIENSUR definir C2 et pas C^(0) ici. (la demo utilises le fait qu'un esenmble inclu dans un espace vectoriel est vectoriel s'il n'est pas vide et stable). Dans cette demo pas besoin d'enumérer les propriété de la loi externe ou besoin de prouver l'assiociativité(ce que tu n'as pas fait en disant qu'il suffisait de dire que c'etait stable par combinaison lineaire et que ca contenait 0).
Quand tu as dit ca je t'ai dit faux, ca c'est suffisant si tu rappelles que c'est inclus dans C2(preuve grace au sous espace vectoriel), si non puisque tu aimes chipoté, c'est insuffisant, il faut enumérer d'autre chose meme si elles sont triviales. Comme que on a bien y*1=y ou encore que si (y1+y2)+y3 est solution alors y1+(y2+y3) associativité de la loi +(ce qui est evident puisque on manipule le groupe (R,+) mais alors dit le, ou encore qu'on manipule l'EV des réels sur R et l'a meme pas besoin de parler des lois externes (mais alors dis le que c'est un EV, ce n'est pas une question de le savoir ou pas, biensur que c'est evident, c'est une question de le preciser. L'exo est simplisime donc evidemment de toute facon que tu ne vas que dire des lapalissades... La n'est pas la question. ) on perd plein de point comme ca tu sais, j'aimerais pas corriger une de tes copies) .

Mais encore une fois tu n'as rien compris et tu t'inventes un monde ou j'ai dit "il faut introduire C2", non DANS CETTE METHODE il faut introduire C2(ca t'evites d'enumerer les conditions de la loi externe qui sont evidemment réalisé pour l'espace vectoriel des réels tout comme quand on dit tout simplement que l'ensemble des réels est un espace vectoriel, c'est tres con peut-etre mais si tu ne le dis pas la demo que tu suggeres est incomplete... Soit tu dis que c'est inclu dans C2 soit tu dis que c'est l'Ev des réels et c'est pas parce que c'est evident qu'il ne faut pas le dire)... Pourquoi j'ai eu l'idée de parler de ca? Juste pour dire que ce que tu disais etait insuffisant quand tu disais qu'il suffisait de dire que cela contenait 0 et que c'etait stable, j'ai dit que cette phrase etait juste si tu disais par exemple que c'etait aussi inclu dans C2 ou encore si tu disais a la place de "c'est inclu dans C2" que les Réel etait un espace vectoriel sur R pour +... Ma demo utilises que c'est de classe C2(si tu trouves que c'est compliqué, la cest un autre probleme). C'est juste une maniere de rendre ta phrase juste. Evidemment que tu peux aussi dire que les réels sont un espace vectoriel pour +,* aussi, mais c'est aussi evident l'un que l'autre, ce n'est pas une question de besoin d'introduire C2 ou pas, ce que tu racontes n'a aucun sens... Si non jepeux te dire, mais tu n'as pas besoin de dire que les réels sont un EV il te suffit de dire que c'est inclu dans C2, tu vois l'absurdité de tes remarques... J'te jure...

Je constate que tu t'en rends compte en tout cas maintenant au moins c'est bien:

Jil suffit de savoir que l'ensemble des fonctions (au départ de n'importe quel ensemble, donc ici on va dire fonctions à variables réelles définies sur un intervalle) à valeurs dans R ou C est un R ou C-espace vectoriel, ce qui vient de la structure de R-espace vectoriel de R, ou de C-espace vectoriel de C (ça fait partie des exemples d'espaces vectoriels de base qu'on voit en L1/maths sup).

Avant tu avais inventé le monde, "tu as besoin de ca pour resoudre l'equadiff, mais tu connais pas ls EV".

Lol on en tiens un la.

Pour le reste tu te repetes et donc j'ai deja tout dit. Ca m'etonnerait pas que tu sois en ecole d'inge toi, apres la prepa vous faites plus grand chose en maths, tu as du un peu oublier donc tu es excusable et puis a pris l'habitude de lire vite apparemment et de pas comprendre ce qu'on te dit... Vraiment un conseil, lis mieux ce que les autres disent et te precipite pas. Essaie de comprendre ce qu'il raconte plutot que ce que tu voudrais entendre. Comme j'ai dit tu aimes t'inventer des idioties a quoi repondre pour te valoriser, les personnes complexées font souvent cela car elle ne peuvent se valoriser sur de veritables sujet, donc elle parle a elle meme comme tu le fais, ou dise "je n'ai pas lu mais je trouve ca quand meme faux" lol...

Tu n'as toujours pas compris pourquoi l'ensemble des solutions d'une équa-diff linéaire homogène du second ordre à coefficients constants est l'ensemble des fonctions de la forme avec r1 et r2 racines de l'équation caractéristique. Recherche la démo dans tes cours de DEUG tu verras bien que ça utilise la structure d'espace vectoriel des solutions.

, je crois que la personne qui ne comprend rien est de l'autre coté du clavier, n'est ce pas? On parle de maths la, si tu veux faire le bonhomme je te suggere d'aller jouer au rugby, j'aurais aimé joué avec toi je suis sur que tu es un grand maniere de la balle . Je n'attends plus de toi que tu comprennes le sens de mes propos au sujet de "la combinaison lineaire". Ce que j'ai remarqué c'est que toi tu fais des maths aproximatifs, un inge surement...

C'est a dire que pour toi un theoreme qui est montré pour y,y',y",y(n) tu en deduis qu'il est aussi valable pour y(t^2). Non monsieur, tu dois le montrer car comme tu peux le voir sur les liens (ou va chercher tes livres de prepa), le theoreme est enoncé pour des variable en t uniquement et pas en f(t) g(t) h(t) differente selon les dérivées. On ne dit pas "il suffit", cette demo tu dois la refaire(tu me dis que tu te souviens de la demo pour y(t) tres bien, tu es fort en math bravo, cette demonstration est considerablmement difficile , et bien ca veut dire que tu serais le prouver mais alors tu dois le faire). Tu as du mal a comprendre la nuance entre c'est vrai ou c'est faux et "il faut le montrer", tout ce qui n'est pas admis(c'est a dire en l'occurence ce n'est surement pas le cas pour un bac+1, ce qui est le cas de celui qui a posé la question) doit etre démontré! C'est pareil pour le reste tu es dans l'aproximatif. De la rigueur et deja tu eviteras de repondre tout le temps a coté, on ne te l'a jamais dit que tu repondais a coté?

bon allé je me retire du sujet bonne soirée ...

Je m'excuse d'avoir rajouter un post apres le dernier, cette fois je te laisse vraiment conclure, je ne peux de toute facon eviter le fait que tu vas indefiniment chercher a avoir raison alors a toi l'honneur.

[abcd22]

Cette methode (tres tres simple) utilise le fait que l'ensemble des solutions est inclus dans un autre espace vectoriel. Mais lequel? Surement pas C0.
Tu as une equation avec du y" et tu me dis qu'on a pas besoin de definir l'espace vectoriel C2 pour cette methode la (regarde bien quel methode j'ai utilisé quand je parle de C2) mdr... L'ensemble de tes solutions "y" la einstein il est pas inclu dans C^(0). Tu as fait un peux d'equa diff apres la prepa? equa aux dérivées partielle, recherche de sol, element fini distribution des trucs comme ca, je pense pas...
[...]
Pour le reste tu te repetes et donc j'ai deja tout dit. Ca m'etonnerait pas que tu sois en ecole d'inge toi, apres la prepa vous faites plus grand chose en maths, tu as du un peu oublier donc tu es excusable et puis a pris l'habitude de lire vite apparemment et de pas comprendre ce qu'on te dit... Vraiment un conseil, lis mieux ce que les autres disent et te precipite pas. Essaie de comprendre ce qu'il raconte plutot que ce que tu voudrais entendre. Comme j'ai dit tu aimes t'inventer des idioties a quoi repondre pour te valoriser, les personnes complexés font souvent cela car elle ne peuvent se valoriser sur de veritables sujet, donc elle parle a elle meme comme tu le fais, ou dise "je n'ai pas lu mais je trouve ca quand meme faux" lol...

:ptdr: C'est vrai ça, pourquoi faire simple quand on peut faire compliqué ? Si si, contrairement à ce que tu dis, l'ensemble des solutions est inclus dans C0, lui-même inclus dans l'ensemble des fonctions d'une variable réelle de R dans R ! Non je suis pas en école d'ingé et je me demande bien comment toi tu peux être en master et ne pas comprendre ce que je reproche à ta méthode de résolution (celle ou tu dis que c'est plus simple de résoudre l'équation pour montrer que l'ensemble des solutions est un espace vectoriel que de le faire directement). Il faut bien que je me répète puisque tu ne comprends pas... mais bon je crois pas que ce soit moi qui dise le plus de choses inutiles ici.

Je m'excuse d'avoir rajouter un post apres le dernier, cette fois je te laisse vraiment conclure, je ne peux de toute facon eviter le fait que tu vas indefiniment chercher a avoir raison alors a toi l'honneur.

C'est plutôt à toi qu'on pourrait dire ça.

PS : Dans un post précédent les 3 points (où tu as répondu que je disais n'importe quoi) ce sont les étapes de la démonstration de la structure des solutions d'une equa-diff linéaire homogène du second ordre à coefficients constants, que j'ai bien vérifiés dans mon cours de prépa, j'irai dire à mon prof qu'il nous a raconté n'importe quoi (je le vois bientôt en plus). Et je parlais bien d'une équa-diff linéaire du second ordre (puisque c'est à ça que tu pensais quand tu as fait ta première réponse et que je voulais te faire remarquer que ton raisonnement se mordait la queue, comme on dit familièrement [#]), pas de l'équation du post initial.

[#] Je te cite : « Cette equation diff est connu et les solutions sont de la forme C1exp(ux) + C2exp(vx)

2)Prouvons que si les solutions s'ecrivent y=C1exp(ux) + C2exp(vx) avec C1 et C2 des réels! alors les solutions forme un espace vectoriel sur R... » tu te rends vraiment pas compte que tu tournes en rond (tu dis : 1) on connait le résultat, 2) le résultat est donc évident !), ni que ce que tu considères comme connu n'est pas complètement trivial (même si c'est vrai qu'on le sait) ?

[MooMooBloo]

Tu es drôle BQss!!
Pourquoi faire simplement un exo alors qu'on peut dire n'importe quoi? :++:

[BQss]

Tu es drôle BQss!!
Pourquoi faire simplement un exo alors qu'on peut dire n'importe quoi? :++:

LOl .

Juste une precision, sur le dernier post effectivement cette fois sur la premiere partie c'est moi qui me suis precipité.
Quand je disais pas inclu dans C^(0), Je voulais dire qu'il n'etait pas inclu dans les fonction uniquement de classe C^(0)(c'est cela dont je parlais et effectivement C0 ce n'est pas cela que ca veut dire, ma faute...), car en suite l'espace d'etude de l'equa diff c'est C2 et que C^(0) est un espace trop grand pour l'etude(les fonctions qui sont "C0 mais pas C2" ne font pas partie des solutions que l'on cherchent), meme si les fonctions de classe C2 sont aussi biensur de classe C(0)... Donc j'ai introduit naturellement par reflexe l'espace C2 car c'est lui l'espace d'etude, et parler d'insuffisance de C0 en pensant a la recherche de solution(alors qu'ici il ne s'agit pas de chercher les solutions mais demontrer qu'il est inclu dansun EV), mea culpa.

C'est pour ca que je disais ca

]C2 ici ne sert qu'a definir un espace contenant l'ensemble des solutions. On ne peut pas definir un espace aussi "grand" que C^(0) dans cet demo car C^(0) dans cette demo ne contient pas les solutions.

Je dis "aussi grand", donc ici j'implique qu'il contient bien C0, mais apres partout ailleurs en disant C0 il faut comprendre "que C0"...
Il faut donc comprendre:
"On ne peut pas definir un espace aussi "grand" que C^(0) dans cet demo car les fonctions qui ne sont que C^(0)(et pas C1,C2...) dans cette demo ne peuvent pas etre solutions..."J'ai été influencé par le fait que C0 est insuffisant pour une recherche efficaces des solutions et definir leur nature...

Mais effectivement ici il ne s'agit pas de rechercher les solutions donc C^(0) en l'occurence est suffisant, on a pas besoin d'un espace vectorielle aussi petit s'il s'agit juste de montrer que les solutions sont inclus dans un autres espace vectoriel plus grand(ce qui etait le sujet de la methode), donc je retire ma remarque la dessus et les eventuelles choses desagreables qui l'ont accompagnés, je pense que ta precipitation est contagieuse abc. J'avoue qu'a force de'entendre n'importe quoi j'en suis rrivé a contredire ce que tu dis par reflexe. Il faut que je fasse gaf effectivement, a parler a un mur on arrive vite a dire soit meme n'importe quoi et je n'ai rien a redire sur le reste de mes interventions ...

Allez cette fois vraiment tchao, beaucoup de bruit pour rien ici... Et jusqu'a ce dernier post, je n'en suis pas le responsable si ce n'est que j'aurai peut-etre du directement passer a autre chose...


PS: les solutions sont de classe C^(infini) meme:
y"(t^2)=-y(t) donc comme comme y" existe y est continue et donc y est de classe C2 d'apres l'égalité--->y est de classe C2 donc comme y"(t^2)=-y(t) y" est aussi de classe C2 et donc y est de classe C4-->y est de classe C4 donc y" est de classe C4 donc y est de classe C6... etc recurrence sur 2n.

lis ca je pense que tu vas enfin comprendre
Et je te rappelle juste que(puisque tu y fais reference):
la methode de recherche de solutions des equa diff n'utilise absolument pas directement le fait que l'equation du second ordre est lineaire et que l'on sait deja que les solutions forme un EV(meme si evidemment c'est lié, ce qui n'est pas la meme chose du tout... C'est a dire qu'on a pas besoin de l'admettre pour trouver les solutions... D'ou le fait qu'on a le droit d'utiliser le resultat sans etre redondant du tout, mais tu as du mal a le comprendre, car comme bcp de chose il y a plein de methode, mais tu as du mal avec le mot methode... Evidemment tu peux n'utiliser que l'ED comme pour la...) . Je te precise la nuance parce que tu butes sur ca je crois.
Dans la demo dont tu parles(precision partout je parle de la demo pour un delta>0 dans l'equation crateristique, pour le reste il ne suffit qu'a changer quelques arguments) il n'y a que la reciproque qui sert. Je m'explique.
On y montre effectivement que toute combinaison lineaire des deux solutions trouvées sont solutions, tres bien, et la on utilise effectivement la propriété lineaire de l'equa diff, mais malheureuseument, c'est la que tu tembrouilles, cela ne veut absolument pas dire que toute les solutions sont des combinaisons lineaire...
C'est dans la deuxieme partie, c'est a dire la reciproque (et cette deuxieme partie ce suffit a elle meme) que la forme generale des solutions est trouvée:
On y pose y=zexp(Ax) avec z une fonction quelquonque. Ainsi y est n'importe qu'elle fonction grace a cette ecriture.

Et on trouve en derivant ce terme puis une deuxieme fois et en remplacant(en utilisant en plus le fait que l'equation caracteristique doit s'annuler decoulant du fait qu'on y a cherché des solutions sous la forme exp(ax) dans un premier temps):
que toute les solutions s'ecrivent sous la forme C1exp(a1x)+C2exp(a2x) C1,C2 réel et donc qu'elles forme un EV.

Nulle part, absoluement nulle part il est necessaire d'utiliser explicitement le fait que l'ED est lineaire ou que les solutions forment un EV pourtant elle abouti a une expression genrale du type C1exp(ax)+C2exp(bx)(i.e cette un demo comme une autre et admise qui montre que l'ensemble des solutions forme un EV... Il ne reste plus qu'a dire que cette forme est celle des elemnts d'un EV, ce que je te dis depuis l'an 40....).

Ca c'est la methode utilisée, celle qui permet en plus d'obtenir les solutions, elle montre que les solutions s'ecrivent sous une combinaison lineaire.
Et donc pour montrer que les solutions sont un espace vectoriel, il suffit(si tu admets ce resultat) d'utiliser cette expression, car elle est connu et de conclure en une ligne... Cela ne veut pas dire qu'elle se suffit a elle meme ni qu'elle ne decoule pas de la linearité de l'ED, mais tout simplement qu'elle est utilisable sans avoir été obligé d'admetter au prealable que les solutions formé un EV, tu comprends la?


Ou alors!!!
TU fais comme pour cette ED la avec y"(t^2) et tu demontres que les solutions forme un EV, cette methode ne mettant pas en meme temps en evidence les solutions exactes, juste que c'est un EV. Elle est plus rapide pour montrer que ce n'est qu'un EV, mais pas plus rapide si on admet le resultat de la premiere(celle qui donne exactement les solutions) et qu'on en deduit a partir de cette combinaison lineaire que l'ensemble des solutions forme un EV(ce resultat qui n'utilise nulle part encore que les sol forment un EV et qui est admis...). Je ne peux pas etre plus clair...

conclusion: si tu utilises les theoremes connus, tu peux dire oui c'est un EV car les sol s'ecrivent comme une Comb lineaires d'apres la demo qui montre les sols exactes.
Et tu ne te mors pas la queue une seconde. Le truc est que avec t^2 cette demo n'existe pas, donc le seul moyen c'est de passer par l'ED, c'est court mais moins court que si l'on sait deja comment s'ecrivent exactement les solutions, ce qui est le cas pour y"(t)... Le probleme c'est que tu confonds le fait que cela aille de paire avec le fait que les solutions forme un EV avec le fait qu'on a pas eu besoin d'utiliser cela, car cette demo qui met en evidence les sol met justement en meme temps en evidence qu'elle forme un EV(il n'y a cas rajouter une ligne: toute combinaison lineaire forme bla bla....)en se laissant guidé et en posant y=ze(ax) on tombe sur ce resultat. Tu confonds cause et consequence et ca c'est pas genial quand on fait des maths...

[abcd22]

je pense que ta precipitation est contagieuse abc. J'avoue qu'a force de'entendre n'importe quoi j'en suis rrivé a contredire ce que tu dis par reflexe. Il faut que je fasse gaf effectivement, a parler a un mur on arrive vite a dire soit meme n'importe quoi et je n'ai rien a redire sur le reste de mes interventions ...

:ptdr: Je vois pas vraiment de précipitation dans mes posts... C'est parce que je fais pas des pavés comme toi ? Moi j'ai toujours à redire sur tes interventions mais je crois que t'es vraiment bouché ou de mauvaise foi.

Allez cette fois vraiment tchao, beaucoup de bruit pour rien ici... Et jusqu'a ce dernier post, je n'en suis pas le responsable si ce n'est que j'aurai peut-etre du directement passer a autre chose...

Ben si... Tu proposes une méthode qui se mord la queue (oui je me répète, je sais), j'estime qu'il faut que quelqu'un le fasse remarquer au moins pour la personne qui a posé la question et les autres qui liront ce fil, même si toi tu ne comprends pas ce qui cloche.

[Gato]

Hello,



est linéaire ; son noyau est un sous-espace vectoriel.

[BQss]

Hello,



est linéaire ; son noyau est un sous-espace vectoriel.

Salut :zen:
Biensur! ce n'est pas la question, je n'ai jamais dit le contraire(il s'agit de methode :marteau: ). C'est juste que moi j'utilise la demo qui donne la forme explicite pour le cas ou c'est y"(t)(cette demo n'utilisant absolument pas le fait que les solutions forme un EV mais au contraire permete entre autre sans le vouloir de montrer ce resultat vu la forme du resultat..., meme si on peut montrer que c'est un EV a partir de l'ED evidemment). Je dis juste que ici comme on ne connait pas la forme explicite des solutions et bien on utilise pas l'allure connu du resultat mais directement l'equation(puisqu'on ne le connait pas), qui permettrait de conclure en une ligne(puisque toute les sol sont combinaison lineaires, ce qui est different de dire que toute combinaison lineaire est solution(nuance importante), je parle bien de toute les sols ici...). Si tu as le courage lis mon PS...

Je precise bien que si on ne sait rien, ca va plus vite de montrer que c'est un EV grace a l'ED directement.
Je disais juste que quand le resultat est connu et admis(pour y"(t) a la place de y"(t^2) par exemple) on peut tres bien dire ba l'ensemble des solutions est comme ca, c'est connu et ce qui s'ecrit comme ca forme un EV(sachant qu'on a pas eu besoin de l'admettre pour trouver la forme generale des solutions). C'est tout absolument tout...

Me:

Citation:
sans avoir été obligé d'admetter au prealable que les solutions formé un EV

YOU:

On ne l'a pas dit, mais on l'a utilisé implicitement, ou on a fait les calculs qui le prouvaient (avec des solutions particulières, mais on utilise juste le fait que ce sont des solutions)...

On cherche des sols sous forme exp, ca nous amene a l'eq caracteristique et on trouve deux sol.
ET d'utiliser une des deux sols dans la demo reciproque(y=zexp(Ax) avec z une fonction quelquonque. Ainsi y est n'importe qu'elle fonction grace a cette ecriture.), puis la relation liant la premiere a la deuxieme(liant deux sol d'un polynome), ca implique qu'on a admis l'existence d'un EV ????
C'est enorme ca! David Coperfield sors de ce corp. Moi je vois juste qu'on utilises les deux seuls resultats connu pour l'instant(le fait de les avoir cherché sous forme d'exp n'a rien a voir avec la presuposition d'un EV...).

Non je suis désolé de te decevoir, mais quand on etablit la forme generale, on a nullement besoin de preciser qu'on manipule des EV, c'est meme la conclusion de la reciproque (H Prepa Analyse premiere année PCSI), ce qui ne change pas le fait que le resultat y est forcement lié, sans blague, c'est sur ca qu'on tombe, heurseusement que c'est lié einstein, t'as deja prouvé deux resultats qui sont pas lié , c'est quoi ca c'est les maths elizabeth Tessier? David Coperfield sors de ce corp ca suffit maintenant.
Et ne fait pas le faut naif sur la reciproque, la premiere partie n'est absolument pas utile pour determiner la nature de l'espace des solutions car la reciproque dit au final bien plus, assis toi je t'explique .
1) l'equation caracteristique, la recherche d'une sol sous forme exp(qui conduit a en trouvé deux et sans posé que c'est un EV) peuvent tres bien etre mise dans la deuxieme partie(elle ne parle pas d'EV) et utilise juste l'ED, (sans blague, on a besoin de l'ED parfois dans la demo c'est enorme ca)

2)ce qui permet de montrer dans la deuxieme partie toujours sans utiliser le fait que les sols forme un EV que si y est solution alors y=C1exp(ax)+C2exp(bx)
et l'honorable Mr Oudot de l'X de conclure la reciproque par " les solutions forment donc un espace vectoriel" mdr quel con celui la on le sait depuis le debut... C'est enorme ca on admet tout le long que c'est un EV et a la fin on tiens bon de rajouter, ca forme donc un EV.

3)La premiere partie montre que les comb lineaire de ces deux sol en exponentielle sont solutions(ce n'est qu'a la fin ou l'on utilise explicitement le fait que l'ED est lineaire, tout le reste se borne a chercher des sols sous forme exponentielle et le polynome de degré deux caracateristique nous en donne deux si D>0, dis donc pas mal je savais pas qu'il y avait besoin d'espace vectoriel la), la deuxieme partie elle, montre que toute solutions est comb lineaire(mais pas n'importe lesquelles et c'est la que la reciproque n'en ai pas vraiment une, car elle implique que TOUTE les combinaisons lineaires sont solutions)... tu dois comprendre la... Ca veut dire que l'equivalence: toute combinaison lineaires de exp(ax) et C2exp(bx)y solution et entierement contenu dans la reciproque.(la premiere partie montre que les combinaison lineaires sont sol, la deuxieme montre que les sols en fait sont n'importe qu'elle combinaison lineaire au lieu de les sols sont des combinaisons lineaires quelquonques meme si c'est ca qu'on cherchait a montré vu que c'est la reciproque.) Et donc ele forment un EV...

Et de plus on se contre fout de savoir que C1exp(ax)+C2exp(bx)-->y solution. Super tu vois ca et tu dis eh oh les amis vous savez quoi je viens de voir un truc qui est sol d'une ED et tu t'amuses meme apres a la construire a partir du a et du b ? Non ca c'est pour la blague bref.

Non nous ce qui nous interesse c'est C1exp(ax)+C2exp(bx)-->y solutions, c.adire la "reciproque", parcequ'elle dit que si y est une solution alors c'est une combinaison lineaire et meme toute et donc que les y forme un espace vectoriel, sacré Oudot il a pas fait l'X pour rien... Je peux te la faire par l'absurde aussi si tu veux:
y solution --> y toutes comb lineaire. Supposons que y pas combinaison lineaire et est solution, aille ca coince hein einstein contradiction, vu que je viens de dire que les sol sont les comb lin, donc tu vois bien la premiere partie bidon bidon je la fous au lac(parce qu'elle ne m'informe pas la dessus comme je l'ai dit), les solutions sont les combinaison lineaire de exp(ax) et exp(bx) .
Si tu dis mais pourquoi on a pas besoin de la reciproque je comprends toujours pas???
Et bien c'est juste que le fait que si toute solutions sont toutes les combinaison lineaire des exponetielle la, ba ca implique directement que tout ce qui est combinaison lineaire de ca est solution, vu que dans la demo C1 et C2 peuvent etre n'importe quel réel(ou complexe), il proviennent de la solutions de deux ED d'odre 1 successive.
La reciproque au final au lieu de dire simplement que les sols sont des combinaisons lineaires quelquonque, en impliquant le fait que cela est vrai pour n'importe quel C1 et C2 du fait qu'il proviennent eux meme de deux ED, fait que les sols sont toutes les combinaisons lineaires et fait que du coup la premiere partie n'a plus d'importance!
Ce qui ne serait pas le cas si on ne savait pas la nature de ce C1 et C2...
En d'autre terme normalement on aurait pour une reciproque normal:

1)toute combinaison est sol donc ensemble des comb est inclu dans l'ensemble des sol
2)Reciproque: Tout sol est une comb donc l'ensemble des sol est inclu dans les comb.

Conclusion Esol=Ecomb

Mais la einstein la reciproque va plus loin et dit carrement, non seuleument que c'est des comb, mais que c'est toute comb, vu que c'est valable pour n'importe quel C1 et C2 réel (si on se place sur les réel par exemple)
Donc en fait la reciproque prouve en meme temps que les sol sont contenus dans l'ensemble des comb et que ces ensembles sont les memes et donc egaux! La premiere partie n'en ai donc pas vraiment une et la reciproque ce suffit a elle meme comme je l'ai dit(si l'on rajoute la partie sur l'equation carateristique qui n'a rien a voir avec les EV). Ca t'ai jamais arrivé de faire une reciproque et de voir que en fait en voulant montré l'autre inclusion tu en arrives a montrer l'egalité? Et bien la c'est ce qui se passe. C'est valable pour tout C1,C2 c'est donc la definition meme d'un EV et plus besoin de premiere partie.

Snif... Heureusement que le jury de l'agrég s'en est pas aperçu.

Tu m'etonnes.

A propos des "lineaire" ce qui n'est pas notre probleme du tout (l'important c'est qu'on a pas besoin d'admettre que les sols forme un EV pour mettre en evidence les sols et tomber jsutement sur la forme d'un EV)
je dis juste que on a pas besoin d'utiliser la condition en la nommant mais juste a utiliser l'ED qui elle meme est evidemment lineaire(c'est pour ca que je dis meme si implicitiment ce resultat est contenu dans l'ED...), ca sert a rien de debattre pour le plaisir la tout lemonde est d'accord et ce n'est pas de ca dont il s'agit... Par contre si tu veux le tel D'Oudot je t'envoies mon mail, il est surement plus pedagogue que moi.

bon cette fois promis je me taille vraiment.
A+ sur d'autre post les amis.

[abcd22]

Dans la demo dont tu parles(precision partout je parle de la demo pour un delta>0 dans l'equation crateristique, pour le reste il ne suffit qu'a changer quelques arguments) il n'y a que la reciproque qui sert. Je m'explique.
On y montre effectivement que toute combinaison lineaire des deux solutions trouvées sont solutions, tres bien, et la on utilise effectivement la propriété lineaire de l'equa diff, mais malheureuseument, c'est la que tu tembrouilles, cela ne veut absolument pas dire que toute les solutions sont des combinaisons lineaire...

Qu'est-ce que ça veut dire « être combinaison linéaire » ? y est combinaison linéaire de y par exemple ? Et « il n'y a que la réciproque qui sert » ? On n'a pas besoin de montrer que les combinaisons linéaires des deux solutions exponentielles sont solution pour montrer que toutes les solutions sont des combinaisons linéaires des exponentielles ? Désolée, comme tu l'as remarqué, je suis débile, je pose des questions à mon niveau...

C'est dans la deuxieme partie, c'est a dire la reciproque (et cette deuxieme partie ce suffit a elle meme) que la forme generale des solutions est trouvée:
On y pose y=zexp(Ax) avec z une fonction quelquonque. Ainsi y est n'importe qu'elle fonction grace a cette ecriture.

Une réciproque peut vivre sans son implication directe donc ?
AAAhhh ! En effet, j'ai pas fait de calculs mais c'est peut-être possible de montrer que toutes les solutions sont de cette forme comme ça (c'est quoi A ?), mais c'est quand même con de faire des calculs quand on peut déduire le résultat directement du théorème de Cauchy (justement tiens, on a un théorème connu, on peut s'en servir).

Nulle part, absoluement nulle part il est necessaire d'utiliser explicitement le fait que l'ED est lineaire

Ben si, tu l'as même reconnu toi-même au-dessus.

sans avoir été obligé d'admetter au prealable que les solutions formé un EV

On ne l'a pas dit, mais on l'a utilisé implicitement, ou on a fait les calculs qui le prouvaient (avec des solutions particulières, mais on utilise juste le fait que ce sont des solutions)...

tu comprends la?

Non, je suis bête, tu pourrais pas m'expliquer les retenues dans les additions plutôt ? Hier j'ai commencé les soustractions, c'est trop dur ! Je crois que j'ai quand même compris un peu au-dessus.

Ou alors!!!
TU fais comme pour cette ED la avec y"(t^2) et tu demontres que les solutions forme un EV, cette methode ne mettant pas en meme temps en evidence les solutions exactes, juste que c'est un EV. Elle est plus rapide pour montrer que ce n'est qu'un EV, mais pas plus rapide si on admet le resultat de la premiere(celle qui donne exactement les solutions) et qu'on en deduit a partir de cette combinaison lineaire que l'ensemble des solutions forme un EV(ce resultat qui n'utilise nulle part encore que les sol forment un EV et qui est admis...). Je ne peux pas etre plus clair...

Ayé, je recomprends plus... T'es sûr de la dernière phrase ?

conclusion: si tu utilises les theoremes connus, tu peux dire oui c'est un EV car les sol s'ecrivent comme une Comb lineaires d'apres la demo qui montre les sols exactes.

Et là le jury te dit « Vous êtes sûr que c'est utile d'utiliser ce théorème ? ».

Tu confonds cause et consequence et ca c'est pas genial quand on fait des maths...

Snif... Heureusement que le jury de l'agrég s'en est pas aperçu.