Définition et unicité du nombre compplexe i

[Lemniscate]

Bonjour,

Je me souviens que dans mon cours de Terminale, on définit i comme le nombre tel que i^2=-1. Et dès lors on admettait que i était unique. Or il est clair que (-i) vérifie (-i)^2=-1. Donc la définition de i ne détermine pas 1 nombre mais 2 !

Cela dit pour passer de l'un à l'autre on a juste à conjuguer...

Voilà ma question : ai-je la bonne définition du nombre i ? Le problème étant qu'on utilise i pour définir toutes les notions du cours (parties réelle et imaginaire, argument, module, conjugué, etc...), on ne peut pas dire comme définition de i : "i est le nombre tel que i^2=-1 et tel que sa partie imaginaire soit positive" ou encore "i est le nombre tel que i^2=-1 et arg(i)=Pi/2 modulo 2Pi".

Merci d'avance pour vos réponses...

Au revoir

[phryte]

Bonjour.
Je pense que la meilleure définition de pi est "un opérateur de rotation de +pi/2".
Exemple : i2 transforme l'abscisse +2 en ordonnée +2
ii2 transforme l'abscisse +2 en abssice -2
...

[phryte]

Bonjour.
C'est le problème de l'aiguille de Buffon :
http://fr.wikipedia.org/wiki/Aiguille_de_Buffon

[Lemniscate]

Merci pour ta réponse mais il me semble que tu définit le plan complexe pour définir i or la définition de plan complexe utilise i. Ca se mord la queue j'ai l'impression !

[Lemniscate]

Bon j'ai demandé à un ami ce qu'il en pensait et il m'a rappelé que le corps des complexes C est isomorphe à R[X]/(X^2+1)
(En effet on consière le morphisme d'anneau g qui à tout élément P de R[X] associe P(i), ce morphisme est surjectif de façon évidente et Ker(g)=(X^2+1), donc lors de la factorisation canonique de g on a un isomorphisme h entre R[X]/(X^2+1) et C.)
Désolé là je dépasse le niveau Lycée ! Peut-être qu'un modérateur pourrait transférer le sujet vers le niveau Supérieur ? Encore désolé...

Cependant la démonstration que je viens de faire utilise déjà le nombre i...

Mais le résultat obtenu ne fait pas intervenir i. On pourrait donc imaginer que i est défini par i=h(T) et que 1=h(U) où T et U uniques dans R[X]/(X^2+1) (Les éléments de R[X]/(X^2+1) sont de la forme aT+bU où T est la classe de X modulo (X^2+1) et U la classe de 1 modulo (X^2+1), donc i=h(T) et 1=h(U), en choisissant h correctement).

Je ne vois pas une meilleure façon de définir i. Peut-être y a-t-il un moyen de définir i correctement sans connaissances postérieures au Lycée ?

A bientôt...

[Timothé Lefebvre]

Désolé là je dépasse le niveau Lycée ! Peut-être qu'un modérateur pourrait transférer le sujet vers le niveau Supérieur ? Encore désolé...

Pas de soucis, c'est fait.

[yos]

Tu peux aussi définir C comme étant R² muni des opérations qu'il faut. Après tu poses i=(0,1). Ca c'est niveau terminale.

[skilveg]

En fait, il n'y a pas de moyen de distinguer algébriquement de son conjugué. Par exemple, si on construit comme le quotient , on peut choisir indifféremment la classe de et celle de 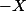comme racine carrée de (la conjugaison est un automorphisme non trivial de ). De la même façon, si on décide d'appeler une clôture algébrique de , cette clôture algébrique est unique à isomorphisme près, mais ces isomorphismes ne sont pas canoniques.

(Et quand on voit comme un opérateur de rotation, il faut choisir un côté du plan où se mettre avant de le faire tourner: l'orientation n'est pas canonique.)

En gros, il se peut très bien que ton interlocuteur travaille avec une autre version de que toi, mais ça ne posera jamais de problème (autre qu'existentiel): les deux versions marchent tout pareil.

Je ne sais pas si je suis très clair :hein:

[Lemniscate]

Salut skilveg,
je dois avouer que j'ai pas vraiment compris ce que tu as expliqué

Déjà :

on peut choisir indifféremment la classe de X et celle de f(x)=x^2 comme racine carrée de f(x)=x^2

On parle bien de classe modulo X^2+1 ? Parles-tu de f(x) en tant que le polynôme X^2 ? qu'entend tu par "racine de f(x)=x^2" (pour moi racine(x^2)=|x| si x réel...)?

la conjugaison est un automorphisme non trivial de C

Que veut dire automorphisme non trivial ? (je sais que trivial=évident mais tu veux dire différent de l'identité ? d'une homothétie ? ...)

clôture algébrique

Késako ? Je vais chercher sur google mais si tu peux l'expliquer ...

isomorphisme canonique

Comment reconnais-tu un isomorphisme canonique d'un autre qui ne l'est pas ? (NB : je sais que canonique = adéquat, adapté et je connais la surjection canonique, bien que je ne vois pas pourquoi on l'appelle comme cela)

il faut choisir un côté du plan où se mettre avant de le faire tourner

C'est quoi pour toi un côté du plan ? Un demi-plan ? Et quand tu fais tourner un plan je vois pas comment, pour une même rotation tu peux obtenir 2 choses différentes.

les deux versions marchent tout pareil.

Est-ce parce que la conjugaison est une isométrie (symétrie par rapport à laxe des réelles) ?

Ok je te pose beaucoup de question mais là j'ai vraiment pas compris ce que t'as voulu dire !

[skilveg]

Bon, mea culpa, je vais essayer de mieux m'exprimer!

1) Là c'est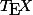 qui fait n'importe quoi, ce que j'ai écrit c'est respectivemen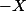t et . (Argh, encore le même problème! et comme ça? 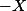(resp. ))

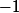2) Non trivial veut dire différent de l'identité. (Par contre, attention, une homothétie est rarement un automorphisme.)

3) Une clôture algébrique d'un corps , c'est une extension (= sur-corps) algébrique de tel que tout polynôme de 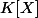soit scindé sur . Exemple: est une clôture algébrique de . D'après un résultat général, deux clôtures algébriques d'un même corps sont isomorphes.

4) Canonique ne veut pas dire grand chose (en tout cas chez moi), mais là je voulais dire que l'isomorphisme dépend éventuellement des choix qu'on fait. En gros, il n'y a pas unicité de l'isomorphisme.

5) Non, je veux dire que si tu visualises le plan comme dans l'espace, il faut l'orienter avant de parler de rotation d'angle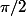 , ce qui revient à choisir un des demi-espaces qui composent le complémentaire du plan (et donc choisir un point de vue par rapport au plan). Je suis d'accord, ce n'est pas génial comme exemple...

6) Je voulais dire qu'elles marchent pareil algébriquement (les calculs dans l'une ou dans l'autre donnent les mêmes résultats) et géométriquement. Donc oui, la conjugaison est une isométrie, et aussi un automorphisme.

J'espère que c'est un peu plus clair... N'hésite pas à demander si tu penses que je peux l'être encore plus ^^

[Lemniscate]

Oui merci, c'est beaucoup plus clair.
Juste une remarque : une homothétie est rarement un automorphise ?!
Là tu remets en cause une connaissance que je pensais sûre à 100% !
Une homothétie, on est d'accord, est une application h dans un K-ev E telle que : ?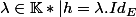
Bon j'ai pris lambda différent de 0, sinon c'est clairement pas un automorphisme. Mais Dans le cas non nul, det(h) different de 0 donc h automorphisme ! Bon après peut-être que tu parles d'espace topologique général ???

Merci en tout cas !

[skilveg]

On s'est mal compris: c'est bien un automorphisme d'espace vectoriel, mais pas un automorphisme de corps si le rapport est différent de 1.

[Lemniscate]

A ok d'accord !
En fait une homothétie n'est pas un morphisme d'anneaux c'est ca ?
parce que si h(x)=ax, h(xy)=axy et h(x)h(y)=a²xy et si a non égal à 1, h(x)h(y) différent de h(xy), c'est ca ?

Bon merci encore, salut

[xyz1975]

C étant isomorphe à R² et l'élément (0,1) à été identifié à i.

[yos]

Variante : définition et unicité du nombre .

[leon1789]

Tu peux aussi définir C comme étant R² muni des opérations qu'il faut. Après tu poses i=(0,1). Ca c'est niveau terminale.

C étant isomorphe à R² et l'élément (0,1) à été identifié à i.

Je trouve que cette manière d'introduire i n'est franchement pas très intuitive. Comment expliquer qu'on prend une multiplication tordue ? Personnellement, plus naturelle me paraît la multiplication composante par composante (comme l'addition). Mais pas de pot, ça ne fait pas ce qu'on veut...

Je préfère largement une définition par générateur (polynômes en i "formel" à coeff dans R) et relation (i²=-1). Avec ça, toutes les opérations sont "normales". On fait comme ça en terminale (sans parler de quotient, ok), et c'est pas mal, non ?

[Lemniscate]

C étant isomorphe à R² et l'élément (0,1) à été identifié à i.

Ok dans ce cas i=f(0,1) où f isomorphisme (d'espaces vectoriels) dont tu parles. Et alors i^2=-1 se traduit par [f(0,1)]^2=-1. On aurait donc une condition multiplicative. Ce qui ne peut se traduire dans R² que si f est un morphisme d'anneau. f(0,1)*f(1,0)=i*1=i et f((0,1)*(1,0))=f(0,0)=0 different de i. Donc il faudrait définir une loi de multiplication sur R², différente de (a,b)*(c,d)=(ab,cd), qui rende f isomorphisme d'anneau... Sinon on ne peut traduire sur (0,1) le fait que i^2=-1 !
Ca me parait bien compliqué en réalité...

Après peut-être qu'en utilisant ce qu'a dit leon1789, on peut s'en sortir.

Variante : définition et unicité du nombre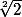

est le nombre a tel que a²=2 et tel que a soit positif. Je ne vois pas en quoi ca pose un problème.

Merci en tout cas de vous pencher sur ma question...

[ThSQ]

Comment expliquer qu'on prend une multiplication tordue ?

Parce que ça marche ? :ptdr:

Plus sérieusement cette méthode se généralise à tout anneau unitaire commutatif auquel on veut ajouter une racine carrée. C'est plutôt cool.

Je préfère largement une définition par générateur (polynômes en i "formel" à coeff dans R) et relation (i²=-1). Avec ça, toutes les opérations sont "normales". On fait comme ça en terminale (sans parler de quotient, ok), et c'est pas mal, non ?

R[X]/(X²+1) ? Perso je préfère celle-là aussi mais elle n'est pas la plus naturelle.

Pourquoi pas la construction à partir de matrices antisymétriques 2x2 ? :marteau:

[Lemniscate]

Pourquoi pas la constructon à partir de matrices antisymétriques 2x2 ?

Merci ! En fait je l'ai vu au début de l'année (enfin très vite en exercice de cours) et je ne m'en rappelais plus (en fait je dois dire qu'à l'époque je n'avais pas compris) !
Bon alors j'ai cherché dans mes notes :

La multiplication marche bien comme dans les complexes, ainsi que l'addition. De plus tout élément s'écrit de façon unique:

Donc et

Merci beaucoup !

[leon1789]

Parce que ça marche ? :ptdr:

:zen:

Plus sérieusement cette méthode se généralise à tout anneau unitaire commutatif auquel on veut ajouter une racine carrée. C'est plutôt cool.

Ben, le passage au quotient A[X]/(X²-a), c'est tout aussi efficace.

R[X]/(X²+1) ? Perso je préfère celle-là aussi mais elle n'est pas la plus naturelle.

Le naturel, c'est très subjectif.

Travailler dans Z modulo n , c'est assez ... "naturel".

Imaginons vouloir construire un anneau commutatif unitaire (sic) dans lequel il existe un élément vérifiant mais avec . Ben c'est pas compliqué :

Travailler dans K[X] modulo P , dans le but de créer une relation désirée (comme ) c'est quand même vachement ... "utile".

Maintenant, comment faire la même chose avec des n-uplets ? (sur l'exemple , sans tricher !)

Pourquoi pas la construction à partir de matrices antisymétriques 2x2 ? :marteau:

peux pas rester sérieux 3 minutes !!! :zen: