Bonjour !
Je fais des exos de maths en plus du cours, mais là je sèche... est-ce que quelqu'un pourrait m'aider ?
Enoncé :
Soit (Xn) une suite réelle. On suppose que les suites (X2n), (X2n+1) et (X3n) convergent. Démontrer que la suite (Xn) converge.
Je ne sais pas si je peux dire que (X2n), (X2n+1) et (X3n) sont des suites extraites de (Xn)...
Je sais que "toute suite extraite d'une suite convergente converge"... mais est-ce que la réciproque est vraie ?
Je pense qu'il va falloir utiliser des théorèmes de suites extraites en tout cas, non ?
Dans le livre, en guise de correction, ils disent : "Considérer les suites extraites (X6n) et (X6n+1)"... cela m'inspire encore moins !!!
A bientôt !
Convergence de suites réelles.
3 messages
- Page 1 sur 1
La réciproque est bien entendu fausse. Ce n'est pas parce que quelques suites extraites converges que la suite converge. Pour s'en convaincre, il suffit de considérer 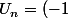^n) . On a bien
. On a bien 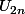 et
et 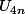 ... qui convergent, mais
... qui convergent, mais  ne converge pas.
ne converge pas.
Si on analyse ce qui t'es donné:
tu sais que la suite (X2n) converge vers , donc que les termes pairs convergent . De même avec la suite impair qui converge vers
, donc que les termes pairs convergent . De même avec la suite impair qui converge vers  . La troisième suite te sert à démontrer que
. La troisième suite te sert à démontrer que 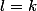 assez simplement, ce qui permet de conclure quant à la convergence de (Xn).
assez simplement, ce qui permet de conclure quant à la convergence de (Xn).
Idée de rédaction pour montrer k=l. On sait que (X3n) converge vers , donc en particulier que toute suite extraite converge vers la même valeur
, donc en particulier que toute suite extraite converge vers la même valeur  . Or, (X6n) est une suite extraite de (X2n) qui converge vers l donc (X6n) converge vers l. D'autre part, (X(6n+3)) est une suite extraite de (X2n+1) et également de (X3n), donc k=l=
. Or, (X6n) est une suite extraite de (X2n) qui converge vers l donc (X6n) converge vers l. D'autre part, (X(6n+3)) est une suite extraite de (X2n+1) et également de (X3n), donc k=l=
Bonne chance
Si on analyse ce qui t'es donné:
tu sais que la suite (X2n) converge vers
Idée de rédaction pour montrer k=l. On sait que (X3n) converge vers
Bonne chance
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
